题目内容
10.把下列各式因式分解(1)2a2-4a
(2)1-36b2
(3)-2a3+12a2-18a;
(4)(a2+6a)2+18(a2+6a)+81.
分析 (1)利用提公因式法和平方差公式,进行因式分解;
(2)利用平方差公式,进行因式分解;
(3)利用提公因式法和完全平方公式,进行分解因式;
(4)利用完全平方公式,进行分解因式.
解答 解:(1)2a2-4a=2a(a-2).
(2)1-36b2=(1+6b)(1-6b).
(3)-2a3+12a2-18a
=-2a(a2-6a+9)
=-2a(a-3)2.
(4)(a2+6a)2+18(a2+6a)+81
=(a2+6a+9)2
=[(a+3)2]2
=(a+3)4.
点评 本题考查了因式分解,解决本题的关键是掌握分解因式的方法.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
1.已知(m-n)2=32,(m+n)2=4000,则m2+n2的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 4032 |
5.如果2x与x-3的值互为相反数,那么x等于( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
15.下列命题中假命题的是( )
| A. | 同位角相等 | |
| B. | 同旁内角互补,两直线平行 | |
| C. | 等角的余角相等 | |
| D. | 过一点能且只能作一条直线和直线平行 |
2.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”,应先假设( )
| A. | 两个锐角都小于45° | B. | 两个锐角都大于45° | ||
| C. | 一个锐角小于45° | D. | 一个锐角小于或等于45° |
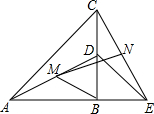 如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.
如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.