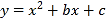Question

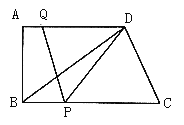
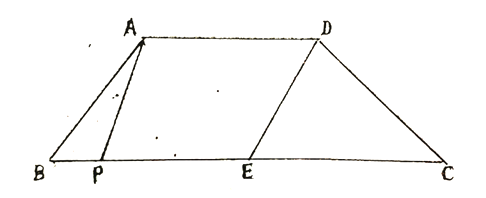
【题目】如图，在梯形中中，，是的中点，，，，，点是边上一动点，设的长为.

（1）当的值为多少时，以点为顶点的三角形为直角三角形；

（2）当的值为多少时，以点为顶点的四边形为平行四边形；

（3）点在边上运动的过程中，以为顶点的四边形能否构成菱形？试说明理由.

Answer 1

【答案】（1）当的值为3或8时，以点为顶点的三角形为直角三角形；（2）当的值为1或11时，以点为顶点的四边形为平行四边形；（3）以点为顶点的四边形能构成菱形，理由详见解析.

【解析】

（1）过AD作于，于，当时，分情况讨论，求出即可；

（2）分为两种情况，画出图形，根据平行四边形的性质推出即可；

（3）化成图形，根据菱形的性质和判定求出BP即可．

解（1）如图，分别过AD作于，于

∴

而

∴

∴

若以为顶点的三角形为直角三角形，

则或，（在图中不存在）

当时

∴与重合

∴

当时

∴与重合

∴

故当的值为3或8时，以点为顶点的三角形为直角三角形；

（2）若以点为顶点的四边形为平行四边形，那么，有两种情况：

①当在的左边，

∵是的中点，

∴

∴

②当在的右边，

故当的值为1或11时，以点为顶点的四边形为平行四边形；

（3）由（2）知，当时，以点为顶点的四边形能构成菱形

当时，以点为顶点的四边形是平行四边形，

∴，过作于，

∵，，则，

∴.

∴，

∴

故此时是菱形

即以点为顶点的四边形能构成菱形.