��Ŀ����
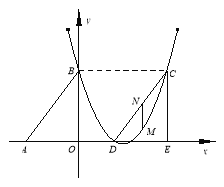
����Ŀ�� ��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��![]() ��0������0��4����������
��0������0��4����������![]() ����B�㣬�Ҷ�����ֱ��
����B�㣬�Ҷ�����ֱ��![]() �ϣ�
�ϣ�

��1����1���������߶�Ӧ�ĺ�����ϵʽ��
��2����2������DCE���ɡ�ABO��x������ƽ�Ƶõ��ģ����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ������������ϣ���˵�����ɣ�
��3����3����M����CD����ֱ���·����������ϵ�һ�����㣬����M��MNƽ����y�ύCD�ڵ�N�����M�ĺ�����Ϊt��MN�ij���Ϊl����l��t֮��ĺ�����ϵʽ������lȡ���ֵʱ����M�����꣮
������
��1����1�������⣬�������������߶�Ӧ�ĺ�����ϵʽΪ![]()
��![]()
��![]()
����������ϵʽΪ��![]()
��2����2����Rt��ABO��OA=3��OB=4��
��![]()
���ı���ABCD������
��BC=CD=DA=AB=5
��C��D���������ֱ��ǣ�5��4������2��0����
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]()
����C�͵�D��������������
��3����3����ֱ��CD��Ӧ�ĺ�����ϵʽΪ![]() ����
����
![]()
��ã�![]() ��
��
��![]()
��MN��y�ᣬM��ĺ�����Ϊt��
��N��ĺ�����ҲΪt��
��![]() ��
�� ![]() ��
��
��![]()
��![]() �� ����
�� ����![]() ʱ��
ʱ��![]() ��
��
��ʱ��M������Ϊ��![]() ��
��![]() ����
����
����������

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
