题目内容
 如图,Rt△ABC中,∠B=90°,BD⊥AC于D,点E为AC的中点,若BC=7,AB=24,则BE=________,BD=________.
如图,Rt△ABC中,∠B=90°,BD⊥AC于D,点E为AC的中点,若BC=7,AB=24,则BE=________,BD=________.
12.5 6.72
分析:根据勾股定理即可求得AC的长,再依据直角三角形斜边上的中线等于斜边的一半,即可求得BE的长;
根据△ABC的面积= AB•BC=
AB•BC= AC•BD即可求解.
AC•BD即可求解.
解答:在直角△ABC中:AC= =
= =25.
=25.
∴BE= AC=12.5;
AC=12.5;
∵△ABC的面积= AB•BC=
AB•BC= AC•BD
AC•BD
∴BD=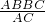 =
= =6.72.
=6.72.
点评:本题主要考查了勾股定理,以及直角三角形的面积的计算方法.
分析:根据勾股定理即可求得AC的长,再依据直角三角形斜边上的中线等于斜边的一半,即可求得BE的长;
根据△ABC的面积=
 AB•BC=
AB•BC= AC•BD即可求解.
AC•BD即可求解.解答:在直角△ABC中:AC=
 =
= =25.
=25.∴BE=
 AC=12.5;
AC=12.5;∵△ABC的面积=
 AB•BC=
AB•BC= AC•BD
AC•BD∴BD=
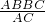 =
= =6.72.
=6.72.点评:本题主要考查了勾股定理,以及直角三角形的面积的计算方法.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.