题目内容
在平面直角坐标系xOy中,一次函数 的图象与反比例函数
的图象与反比例函数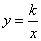 的图象的一
的图象的一
个交点为A(1,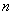 ).
).
(1)求反比例函数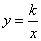 的解析式;
的解析式;
(2)若P是坐标轴上一点(P不与O重合),且满足 ,直接写出点P的坐标.
,直接写出点P的坐标.
⑴ ∵点A(1,n)在一次函数 的图象上,
的图象上,
∴n=3.
∴点A的坐标为(1,3).
∵点 的反比例函数
的反比例函数 的图象上,
的图象上,
∴k=3.
∴反比例函数的解析式为 .
.
⑵ 点P的坐标为(2,0)或(0,6).

阅读下面资料:
小明遇到这样一个问题:如图1,对面积为a的△ABC逐次进行以下操作:分别延长AB、
BC、CA至A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,
得到△A1B1C1,记其面积为S1,求S1的值.
小明是这样思考和解决这个问题的:如图2,连接A1C、B1A、C1B,因为A1B=AB,
B1C=BC,C1A=CA,根据等高两三角形的面积比等于底之比,

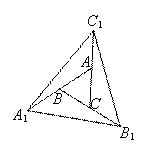
图1 图2
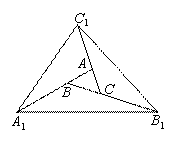
所以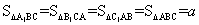 ,由此继续推理,从而解决了这个问题.
,由此继续推理,从而解决了这个问题.
(1)请直接写出S1= ;(用含字母a的式子表示).
请参考小明同学思考问题的方法,解决下列问题:
(2)如图3,对面积为a的△ABC逐次进行以下操作:分别延长AB、BC、CA至A1、
B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其
面积为S2,求S2的值.
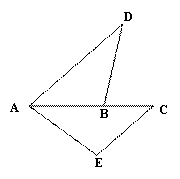
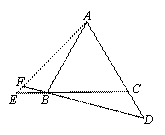
(3)如图4,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于
点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,设△APE的面积为y,△BPF的面积为x,
①求△APE ,△BPF,△APF 面积之间的关系;
②求△ABC的面积.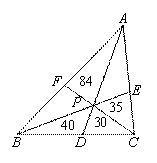
|
| ||||
为了解居民用水情况,晓娜在某小区随机抽查了10户家庭的月用水量,结果如下表:
| 月用水量(吨) | 5 | 6 | 7 | 8 | 9 | 10 |
| 户数 | 1 | 1 | 2 | 2 | 3 | 1 |
则这10户家庭的月用水量的平均数和众数分别是
A.7.8,9 B.7.8 ,3 C.4.5,9 D.4.5,3
,3 C.4.5,9 D.4.5,3
 中,
中, ,以
,以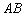 为直径作⊙
为直径作⊙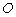 ,交
,交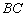 于点
于点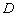 ,连接
,连接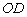 ,过点
,过点 ,交
,交 于点
于点 。
。 ;
; ,
, 时,求
时,求 及
及 的长。
的长。
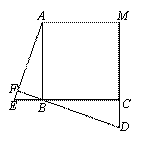
 图,正三角形ABC、正四边形ABCM、正五边形ABCMN中,点E在CB的延长线
图,正三角形ABC、正四边形ABCM、正五边形ABCMN中,点E在CB的延长线 AFB度数为 , 若将条件“正三角形、
AFB度数为 , 若将条件“正三角形、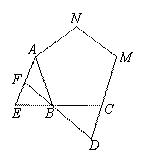
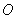 是△
是△ 的外接圆,
的外接圆, ,连结
,连结 并延长交⊙
并延长交⊙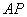 于点
于点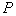 .
. ;
; (2)若
(2)若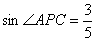 ,
,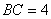 ,求
,求