题目内容
如图，已知直线AC∥DE，∠C=35°，∠E=65°，则∠B的度数是
- A.30°
- B.40°
- C.50°
- D.100°
A
分析：根据平行线性质得到∠BAF=∠E=65°，然后利用三角形外角性质得到∠BAF=∠C+∠B，再把∠C=35°，∠BAF=65°代入计算即可．
解答：如图，
∵AC∥DE，
∴∠BAF=∠E=65°，
又∵∠BAF=∠C+∠B，∠C=35°，
∴∠B=65°-35°=30°．
故选A．
点评：本题考查了平行线的性质：两直线平行，同位角相等．也考查了三角形外角性质．
分析：根据平行线性质得到∠BAF=∠E=65°，然后利用三角形外角性质得到∠BAF=∠C+∠B，再把∠C=35°，∠BAF=65°代入计算即可．
解答：如图，
∵AC∥DE，
∴∠BAF=∠E=65°，
又∵∠BAF=∠C+∠B，∠C=35°，
∴∠B=65°-35°=30°．
故选A．
点评：本题考查了平行线的性质：两直线平行，同位角相等．也考查了三角形外角性质．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
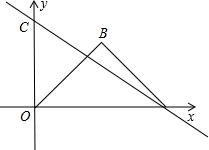角形，∠B=90°，抛物y=mx2+3x过点B，将△OAB绕点O顺时针旋转，使点B落在直线AC上的点B′处．
20、如图，已知直线AC和直线BD相交于点O，OA=OB，请你添加一个使OC=OD的条件，并证明．
（2011•花都区二模）如图，已知直线AC∥DE，∠C=35°，∠E=65°，则∠B的度数是（ ）
如图，已知直线AC，D是AC上的点，AB∥CE，CE平分∠DAC，判断∠A与∠B的大小关系，并说明理由．
交两坐标轴于点A、C，△OAB是等腰直角三角形，∠B=90°，抛物y=mx2+3x过点B，将△OAB绕点O顺时针旋转，使点B落在直线AC上的点B′处．