Question

如图，已知直线AC：y=-

3

3

x+

2

3

3

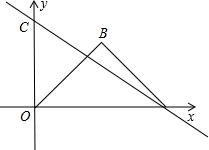交两坐标轴于点A、C，△OAB是等腰直角三角形，∠B=90°，抛物y=mx²+3x过点B，将△OAB绕点O顺时针旋转，使点B落在直线AC上的点B′处．
（1）求m的值；
（2）点B′的坐标，并说明点B′是否在抛物线上；
（3）求线段BB′的长．

Answer 1

分析：（1）要求m的值，先要求出B的坐标，即先要求出OA的长，已知了直线AC的解析式，那么不难得出A的坐标应该是（2，0），OA=2，那么B的坐标应该是（1，1）．将B的坐标代入二次函数的解析式中即可得出m的值．
（2）可过B′作B′D⊥OA于D，那么B′O=OB=

2

，B′D的长就是B′的纵坐标，OD的长就是B′的横坐标，由于B′D是直角三角形OB′D和AB′D的公共直角边，可围绕这条直角边，分别在两个三角形中用OD表示出B′D的长，进而可求出OD和B′D的长，也就得出了B′的坐标，然后将B′的坐标代入二次函数的解析式中判定B′是否在抛物线上．
（3）已知了B、B′的坐标可根据坐标系中两点距离的公式进行求解即可．

解答：解：（1）由于A是直线AC与x轴的交点，则A点的坐标应是（2，0）．
由于△OBA是等腰直角三角形，
因此BD点的坐标应该是（1，1），
将B点的坐标代入y=mx²+3x中，
则m+3=1，即m=-2，

（2）过B′作B′D⊥OA于D，设OD=a，
直角三角形OB′D中，OB′=OB=

2

，
根据勾股定理可得：B′D²=2-x²，
直角三角形B′DA中，AD=OA-OD=2-x，tan∠A=

B′D

AD

=

2 3 3

2

，
因此B′D=

3

3

（2-x），
因此：B′D²=2-x²=

1

3

（2-x）²
解得x=

1+ 3

2

（线段长不为负数，因此将负值舍去），
因此B′D=

2 2-( 1+ 3 2 )2

=

3 -1

2

，
因此B′的坐标是（

3 +1

2

，

3 -1

2

），
由（1）知抛物线的解析式为y=-2x²+3x．
当B′=

1+ 3

2

时，y=-2×（

1+ 3

2

）²+3×

1+ 3

2

=

3 -1

2

，
因此B′在抛物线上．

（3）因为B点的坐标是（1，1），B′的坐标是（

3 +1

2

，

3 -1

2

），
因此BB′=

( 1+ 3 2 -1)2+( 3 -1 2 -1)2

=

3

-1．

点评：本题结合了三角形的相关知识考查一次函数及二次函数的综合应用，
（2）中求B′坐标时，构建直角三角形运用好两直角三角形的公共直角边是解题的关键．