题目内容
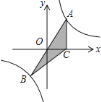
【题目】如图，已知经过原点的直线
与反比例函数
图象分别相交于点
和点
，过点作
轴于点
，若
的面积为
，则
的值为（ ）
A. 2 B. 4 C. 6 D. 8
【答案】B
【解析】
首先根据反比例函数与正比例函数的图象特征，可知A、B两点关于原点对称，则O为线段AB的中点，故△BOC的面积等于△AOC的面积，都等于2，然后由反比例函数y=
的比例系数k的几何意义，可知△AOC的面积等于
|k|，从而求出k的值．
解：∵反比例函数与正比例函数的图象相交于A、B两点，
∴A、B两点关于原点对称，
∴OA=OB，
∴△BOC的面积=△AOC的面积=4÷2=2，
又∵A是反比例函数y=图象上的点，且AC⊥x轴于点C，
∴△AOC的面积=|k|，
∴|k|=2，
∵k＞0，
∴k=4．
故选：B．
练习册系列答案
名校通行证有效作业系列答案
相关题目
