Question

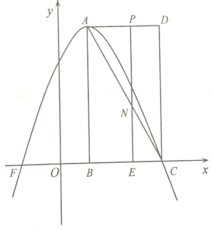
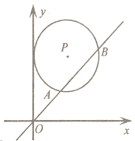
【题目】如图，在平面直角坐标系中，与轴相切，直线被截得的弦长为，若点的坐标为，则的值为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

过点P作PH⊥AB于H，PD⊥x轴于D，交直线y=x于E，连结PA，根据切线的性质得PC⊥y轴，则P点的横坐标为4，所以E点坐标为（4，4），易得△EOD和△PEH都是等腰直角三角形，根据垂径定理由PH⊥AB得AH=，根据勾股定理可得PH=2，于是根据等腰直角三角形的性质得PE=，则PD=，然后利用第一象限点的坐标特征写出P点坐标．

解：过点P作PH⊥AB于H，PD⊥x轴于D，交直线y=x于E，连结PA，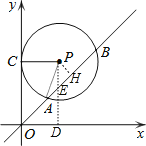

∵⊙P与y轴相切于点C，
∴PC⊥y轴，
∴P点的横坐标为4，
∴E点坐标为（4，4），
∴△EOD和△PEH都是等腰直角三角形，
∵PH⊥AB，
∴AH=，
在△PAH中，PH=，
∴PE=，
∴PD= ，
∴P点坐标为（4，）．

故选：B