题目内容
 如图,一次函数y=kx+b的图象交x轴于点A(4,0),与y轴正半轴交于点B,cos∠BAO=
如图,一次函数y=kx+b的图象交x轴于点A(4,0),与y轴正半轴交于点B,cos∠BAO=| 4 |
| 5 |
(1)求一次函数的解析式;
(2)OC是△AOB的角平分线,反比例函数y=
| m |
| x |
考点:一次函数综合题
专题:综合题
分析:(1)由A的坐标得到OA的长,在直角三角形AOB中,根据cos∠BAO的值及OA的长,利用锐角三角函数定义求出OB的长,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)由OC为∠AOB的平分线,且∠AOB为直角,判断得到三角形OCD为等腰直角三角形,即CD=OD=a,表示出C坐标,代入一次函数解析式求出a的值,确定出C坐标,将C坐标代入反比例解析式求出m的值即可.
(2)由OC为∠AOB的平分线,且∠AOB为直角,判断得到三角形OCD为等腰直角三角形,即CD=OD=a,表示出C坐标,代入一次函数解析式求出a的值,确定出C坐标,将C坐标代入反比例解析式求出m的值即可.
解答: 解:(1)∵A(4,0),∴OA=4,
解:(1)∵A(4,0),∴OA=4,
∵∠AOB=90°,cos∠BAO=
,
∴AB=
=5,
∴OB=
=3,即B(0,3),
将A(4,0)和B(0,3)代入y=kx+b得:
,
解得:
,
则一次函数解析式为y=-
x+3;
(2)过C作CD⊥OA,设OD=a,
∵OC平分∠AOB,∠AOB=90°,
∴∠COD=
∠AOB=45°,
∵CD⊥OA,
∴△CDO为等腰直角三角形,
∴CD=OD=a,即C(a,a),
∵C点在直线AB上,
将C坐标代入直线AB得:-
a+3=a,
解得:a=
,
∴C(
,
),
将C坐标代入反比例解析式得:m=
.
 解:(1)∵A(4,0),∴OA=4,
解:(1)∵A(4,0),∴OA=4,∵∠AOB=90°,cos∠BAO=
| 4 |
| 5 |
∴AB=
| OA |
| cos∠BAO |
∴OB=
| AB2-OA2 |
将A(4,0)和B(0,3)代入y=kx+b得:
|
解得:
|
则一次函数解析式为y=-
| 3 |
| 4 |
(2)过C作CD⊥OA,设OD=a,
∵OC平分∠AOB,∠AOB=90°,
∴∠COD=
| 1 |
| 2 |
∵CD⊥OA,
∴△CDO为等腰直角三角形,
∴CD=OD=a,即C(a,a),
∵C点在直线AB上,
将C坐标代入直线AB得:-
| 3 |
| 4 |
解得:a=
| 12 |
| 7 |
∴C(
| 12 |
| 7 |
| 12 |
| 7 |
将C坐标代入反比例解析式得:m=
| 144 |
| 49 |
点评:此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,等腰直角三角形的判定与性质,坐标与图形性质,以及反比例函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a3-a2=a |
| B、a8÷a2=a4 |
| C、(3a)3=9a3 |
| D、(a3)2=a6 |
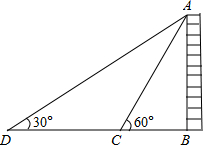 如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?
如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?
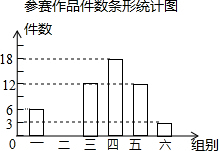 某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答:
某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答: