Question

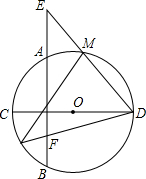如图，AB是⊙O的弦，CD是⊙O的直径，AB⊥CD，过点D作直线交BA的延长线于E，交⊙O于点M，点N为

BC

上任意一点，连接DN交AB于F．
（1）已知DM=

2

，cos∠BED=

4

5

，求⊙O的半径；
（2）求证：DN•DF=DE•MD．

Answer 1

分析：（1）连接CM，由于CD是⊙O的直径，所以∠CMD=90°，再由AB⊥CD可得出∠E+∠CDM=90°，进而可的得出∠C=∠BED，所以cos∠C=cos∠E=

4

5

，设CM=4x，则CD=5x，由勾股定理可知MD=3x，再根据DM=

2

可求出x的值，故可求出CD的值，进而得出结论；
（2））根据∠DCM=∠E，∠DCM=∠N可知∠N=∠E，再由∠MDN=∠EDF，可得出△NDM∽△EDF，根据相似三角形的对应边成比例即可得出结论．

解答：（1）解：连接CM，
∵CD是⊙O的直径，
∴∠CMD=90°，
∵AB⊥CD，
∴∠E+∠CDM=90°，
又∵∠DCM+∠CDM=90°，
∴∠C=∠BED，
∴cos∠C=cos∠E=

4

5

，
∴设CM=4x，则CD=5x，
∴MD=

CD2-CM2

=

(5x)2-(4x)2

=3x，
∵DM=

2

，
∴x=

2

3

，
∴CD=

5 2

3

，
∴⊙O的半径为

5 2

6

；

（2）∵∠DCM=∠E，∠DCM=∠N，
∴∠N=∠E，
又∵∠MDN=∠EDF，
∴△NDM∽△EDF，
∴

DN

DE

=

DM

DF

，
∴DN•DF=DE•MD．

点评：本题考查的是圆的综合题，涉及到圆周角定理、相似三角形的判定与性质、勾股定理等相关知识，难度适中．