题目内容
直线
分别与x轴、y轴交于 B、A两点。
（1）求B、A两点的坐标；
（2）把△AOB以直线AB为轴翻折，点O落在平面上的点C处，以BC为一边作等边△BCD 求D点的坐标。
分别与x轴、y轴交于 B、A两点。（1）求B、A两点的坐标；
（2）把△AOB以直线AB为轴翻折，点O落在平面上的点C处，以BC为一边作等边△BCD 求D点的坐标。
解：如图（1）令x=0，由 得y=1 令y=0，由  ，得 ，∴B点的坐标为（  ，0），A点的坐标为（0，1）；（2）由（1）知OB=  ，OA=1，∴tan∠OBA=  ，∴∠OBA=30°， ∵△ABC和△ABO关于AB成轴对称， ∴BC=BO=  ，∠CBA=∠OBA=30°，∴∠CBO=60°， 过点C作CM⊥x轴于M，则在Rt△BCM中 CM=BC×sin∠CBO=  ×sin60°= BM=BC×cos∠CBO=  ×cos60°= ∴OM=OB-BM=  ，∴C点坐标为（  ），连结OC， ∵OB=CB，∠CBO=60°， ∴△BOC为等边三角形， 过点C作CE∥x轴，并截取CE=BC则∠BCE=60°， 连结BE则△BCE为等边三角形， 作EF⊥x轴于F，则EF=CM=  ，BF=BM= OF=OB+BF=  ，∴点E坐标为（  ），∴D点的坐标为（0，0）或（  ）。 |
 |
练习册系列答案
相关题目
已知：如图，直线y=-x+4分别与x轴，y轴交于A、B两点，从点P（2，0）射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是（ ）
B，⊙P经过点A、点B（圆心P在x轴负半轴上），已知AB=10，
（2012•青浦区二模）如图，直线y=x+1分别与 x轴、y轴分别相交于点A、B．抛物线y=ax2+bx+c（a≠0）与 y轴的正半轴相交于点C，与这个一次函数的图象相交于A、D，且sin∠ACB=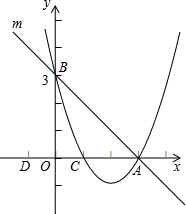
（2013•澄江县二模）如图，已知：直线m分别与x轴、y轴相交于A、B两点，抛物线y=ax2+bx+c经过A（3，0）、B（0，3）、C（1，0）三点．
分别与x轴、y轴相交于A、B两点，O为坐标原点，A点的坐标为（4，0）。