题目内容
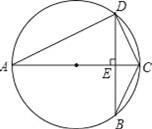
如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE•AC,求证:CD=CB.
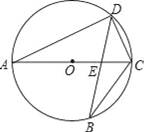

【考点】圆周角定理;相似三角形的判定与性质.
【专题】证明题.
【分析】(1)由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠B,又由对顶角相等,可证得:△ADE∽△BCE;
(2)由AD2=AE•AC,可得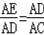
 ,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,以求得AC⊥BD,由垂径定理即可证得CD=CB.
,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,以求得AC⊥BD,由垂径定理即可证得CD=CB.
【解答】证明:(1)如图,∵∠A与∠B是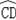
 对的圆周角,
对的圆周角,
∴∠A=∠B,
又∵∠1=∠2,
∴△ADE∽△BCE;
(2)如图,
∵AD2=AE•AC,
∴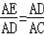
 ,
,
又∵∠A=∠A,
∴△ADE∽△ACD,
∴∠AED=∠ADC,
又∵AC是⊙O的直径,
∴∠ADC=90°,
即∠AED=90°,
∴直径AC⊥BD,
∴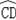
 =
=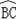
 ,
,
∴CD=CB.

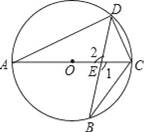

【点评】此题考查了圆周角定理、垂径定理一相似三角形的判定与性质.此题难度不大,注意数形结合思想的应用.

练习册系列答案
相关题目
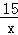 的图象经过点C.
的图象经过点C.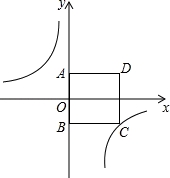

 (x>0)的图象经过顶点B,则k的值为 .
(x>0)的图象经过顶点B,则k的值为 .


 B.
B.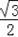
 C.
C.



 =1,则 ( )
=1,则 ( ) 2 C. x≠
2 C. x≠ D. x为任意有理数
D. x为任意有理数  = .
= .
