Question

24、如图△ABC为等边三角形，直线a∥AB，D为直线BC上任一动点，将一60°角的顶点置于点D处，它的一边始终经过点A，另一边与直线a交于点E．
（1）若D恰好在BC的中点上（如图1）求证：△ADE是等边三角形；
（2）若D为直线a上任一点（如图2），其他条件不变，上述（1）的结论是否成立？若成立，请给予证明；若不成立，请说明理由．

Answer 1

分析：（1）根据题意得出EC=CD=DB，进而可证得△ABD≌△ACE，从而可判断出结论．
（2）在BC上截取CF，使DF=BC，从而证得△ABD≌△DFE，进而得出结论．

解答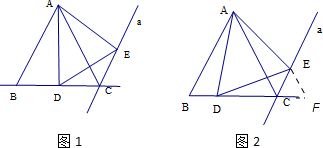：（1）证明：∵a∥AB，且△ABC为等边三角形，
∴∠ACE=∠BAC=∠ABD=60°，AB=AC，
∵BD=CD，
∴AD⊥BC
∵∠ADE=60°，
∴∠EDC=30°，
∴∠DOC=180°-∠EDC-∠ACB=90°，
∴∠DEC=∠DOC-∠ACE=30°，
∴∠EDC=∠DEC，
∴EC=CD=DB，
∴△ABD≌△ACE．
∴AD=AE，且∠ADE=60°，
∴△ADE是等边三角形；

（2）在BC上截取CF，使DF=BC，
∴BC-DC=DF-DC，即BD=CF，
由（1）△ABD≌△ACE得到BD=CE，
∴EC=FC，
又CE∥AB，∴∠ECF=60°，
∴△CEF为等边三角形，
∠EDF+60°=∠BAD+60°，
∴∠EDF=∠BAD，
又DF=BC=AB，
∴△ABD≌△DFE，
∴AD=DE，即△ADE是等边三角形．

点评：本题考查了等边三角形的判定及性质，难度较大，注意基本性质的掌握及熟练应用是解答本题的关键．