题目内容
17.在平面直角坐标系中,抛物线y=ax2-2ax+c与x轴交于A、B两点(A点在B点左侧),且AB=4,与y轴正半轴交于C点,OC=OB.(1)求抛物线的解析式;
(2)直接写出该抛物线的顶点坐标(1,4),与x轴交点坐标为(-1,0)(3,0).
(3)抛物线上点(-2,b)在图象上的对称点的坐标是(4,b).
分析 (1)根据抛物线y=ax2-2ax+c可求得对称轴,然后根据抛物线关于对称轴对称,与x轴交于A、B两点(A点在B点左侧),且AB=4,与y轴正半轴交于C点,OC=OB,从而可以得到A、B、C三点的坐标,从而可以求得抛物线的解析式;
(2)根据第一问可以求得该问的答案;
(3)根据抛物线关于对称轴对称,可以求得抛物线上点(-2,b)在图象上的对称点的坐标.
解答 解;(1)∵抛物线y=ax2-2ax+c,
∴抛物线的对称轴为:x=$-\frac{-2a}{2a}=1$.
∵抛物线y=ax2-2ax+c与x轴交于A、B两点(A点在B点左侧),且AB=4,与y轴正半轴交于C点,OC=OB,
∴点A的坐标为(-1,0),点B的坐标为(3,0),点C的坐标为(0,3).
∴$\left\{\begin{array}{l}{a+2a+c=0}\\{9a-6a+c=0}\\{c=3}\end{array}\right.$,
解得a=-1,c=3.
∴抛物线的解析式为:y=-x2+2x+3.
(2)∵由(1)可知抛物线的对称轴为:x=1,
∴将x=1代入y=-x2+2x+3得,y=4.
∴该抛物线的顶点坐标为(1,4).
由(1)知抛物线与x轴的两个交点坐标分别为:(-1,0),(3,0).
故答案为:(1,4),(-1,0),(3,0).
(3)∵该抛物线关于直线x=1对称,
∴抛物线上点(-2,b)在图象上的对称点的坐标是(4,b).
故答案为:(4,b).
点评 本题考查抛物线与x轴的交点、与y轴的交点,抛物线关于对称轴对称,解题的关键是找出所求问题需要的条件,灵活变化,根据题目中的已知条件进行转化.

练习册系列答案
相关题目
7.下面运算正确的是( )
| A. | 3ab+3ac=6abc | B. | 4a2b-4b2a=0 | C. | 2x2+5x2=7x4 | D. | 5y2-2y2=3y2 |
12.下列说法:(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;(3)全等三角形的周长相等;(4)周长相等的两个三角形相等;(5)全等三角形的面积相等;(6)面积相等的两个三角形全等.其中不正确的是( )
| A. | (4)(5) | B. | (4)(6) | C. | (3)(6) | D. | (3)(4)(5)(6) |
6.我国的陆地面积为9600000平方千米,9600000用科学记数法可表示为( )
| A. | 96×105 | B. | 9.6×106 | C. | 0.96×107 | D. | 960×104 |
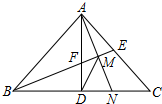 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;
如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;