题目内容
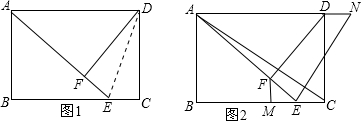
如图,将矩形ABCD的一边CD沿DE折叠,使点C落在AE上,
(1)如图1,若折痕DE=2 ,且tan∠DAF=
,且tan∠DAF= ,求矩形ABCD的周长;
,求矩形ABCD的周长;
(2)如图2,过点F作FM∥AB,交BC于M,在AD边的延长线上截取DN=EM,连接EN、AC.求证:AC⊥EN.
解:(1)由 tan∠DAF= ,可设DF=3x,AF=4x,
,可设DF=3x,AF=4x,
在Rt△ADF中,AD= =5x,
=5x,
由矩形及折叠的性质可得:CD=DF=AB,
∵在△ADF和△AEB中,
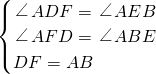 ,
,
∴△ADF≌△EAB,
∴AE=AD=5x,BE=AF=4x,
∴EC=BC-BE=AD-BE=x,
在△DCE中,DE2=CE2+CD2,即(2 )2=x2+(3x)2,
)2=x2+(3x)2,
解得:x= ,
,
则矩形的周长为=2(AB+AD)=16x=16 .
.
(2)连接DM交AC于H,延长DF交BC于K,
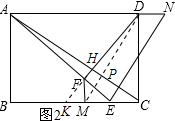
∴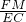 =
=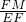 =
= =
=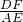 ,
,
∵∠KFM=∠FEM(同角的余角相等,都是∠EFM的余角),
∴∠DFM=∠AEC(等角的补角相等),
∴△DFM∽△AEC,
∴∠EAC=∠FDM,
∵∠EAC+∠AHF=90°,∠AHF=∠DHP,
∴∠FDM+∠DHP=90°,
∴DM⊥AC,
∵DN ME,
ME,
∴四边形DMEN是平行四边形,
∴AC⊥EN.
分析:(1)设DF=3x,AF=4x,可求出AD,证明△ADF≌△EAB,从而确定EC的长度,在Rt△DCE中利用勾股定理可求出x的值,继而得出矩形的周长;
(2)连接DM交AC于H,延长DF交BC于K,通过证明△DFM∽△AEC,得到∠EAC=∠FDM,继而证明DM⊥AC,容易判断四边形DMEN是平行四边形,继而可得结论.
点评:本题考查了翻折变换的知识,涉及了全等三角形的判定与性质、相似三角形的判定与性质及平行四边形的判定,综合性较强,解答本题需要将所学的知识融会贯通.
 ,可设DF=3x,AF=4x,
,可设DF=3x,AF=4x,在Rt△ADF中,AD=
 =5x,
=5x,由矩形及折叠的性质可得:CD=DF=AB,
∵在△ADF和△AEB中,
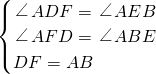 ,
,∴△ADF≌△EAB,
∴AE=AD=5x,BE=AF=4x,
∴EC=BC-BE=AD-BE=x,
在△DCE中,DE2=CE2+CD2,即(2
 )2=x2+(3x)2,
)2=x2+(3x)2,解得:x=
 ,
,则矩形的周长为=2(AB+AD)=16x=16
 .
.(2)连接DM交AC于H,延长DF交BC于K,

∴
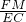 =
=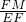 =
= =
=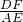 ,
,∵∠KFM=∠FEM(同角的余角相等,都是∠EFM的余角),
∴∠DFM=∠AEC(等角的补角相等),
∴△DFM∽△AEC,
∴∠EAC=∠FDM,
∵∠EAC+∠AHF=90°,∠AHF=∠DHP,
∴∠FDM+∠DHP=90°,
∴DM⊥AC,
∵DN
 ME,
ME,∴四边形DMEN是平行四边形,
∴AC⊥EN.
分析:(1)设DF=3x,AF=4x,可求出AD,证明△ADF≌△EAB,从而确定EC的长度,在Rt△DCE中利用勾股定理可求出x的值,继而得出矩形的周长;
(2)连接DM交AC于H,延长DF交BC于K,通过证明△DFM∽△AEC,得到∠EAC=∠FDM,继而证明DM⊥AC,容易判断四边形DMEN是平行四边形,继而可得结论.
点评:本题考查了翻折变换的知识,涉及了全等三角形的判定与性质、相似三角形的判定与性质及平行四边形的判定,综合性较强,解答本题需要将所学的知识融会贯通.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
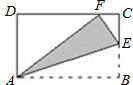 如图,将矩形ABCD的BC边折起,使点B落在DC上的点F处得折痕AE,若∠DFA为40°,则∠EAF的度数是( )
如图,将矩形ABCD的BC边折起,使点B落在DC上的点F处得折痕AE,若∠DFA为40°,则∠EAF的度数是( )| A、15° | B、20° | C、25° | D、30° |
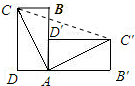 如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=2DA=2,那么CC′=
如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=2DA=2,那么CC′= 4、如图,将矩形ABCD折叠,AE是折痕,点D恰好落在BC边上的点F处,量得∠BAF=50°,那么∠DEA等于( )
4、如图,将矩形ABCD折叠,AE是折痕,点D恰好落在BC边上的点F处,量得∠BAF=50°,那么∠DEA等于( ) 12、如图,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,∠GFP=62°,那么∠EHF的度数等于
12、如图,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,∠GFP=62°,那么∠EHF的度数等于 如图,将矩形ABCD绕C点顺时针旋转到矩形CEFG,点E在CD上,若AB=8,BC=6,则旋转过程中点A所经过的路径长为
如图,将矩形ABCD绕C点顺时针旋转到矩形CEFG,点E在CD上,若AB=8,BC=6,则旋转过程中点A所经过的路径长为