题目内容
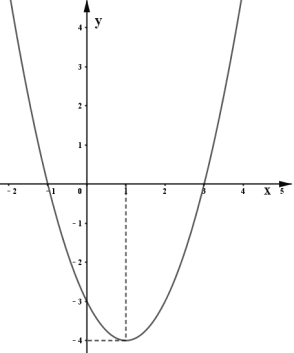
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() ,
,![]() 两点,
两点,![]() 为抛物线上一动点(不与
为抛物线上一动点(不与![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方时,过点
下方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的最大值是
的最大值是![]() ;(3)能,点
;(3)能,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 或
或![]() .
.
【解析】
(1)把B(3,0),C(0,2)代入![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)设P(m,![]() ),得到N(m,
),得到N(m,![]() ),
),![]() ,由两点间的距离公式得到关于m的二次函数,根据二次函数的性质即可得到结论;
,由两点间的距离公式得到关于m的二次函数,根据二次函数的性质即可得到结论;
(3)求得E(0,![]() ),得到CE=
),得到CE=![]() ,设P(m,
,设P(m,![]() ),①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到G(0,
),①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到G(0,![]() ),设P(m,
),设P(m,![]() ),则F(m,
),则F(m,![]() ),列方程得到此方程无实数根,于是得到结论.
),列方程得到此方程无实数根,于是得到结论.
解:(1)把![]() ,
,![]() 代入
代入![]() 得
得 ,
,
∴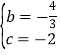 .
.
∴抛物线的解析式为:![]() .
.
(2)设![]() ,
,
∵![]() 轴,
轴,![]() 轴,
轴,![]() ,
,![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() 的最大值是
的最大值是![]() ;
;
(3)能,
理由:∵![]() 交y轴于点E,
交y轴于点E,
∴E(0,![]() ),
),
∴CE=![]() ,
,
设P(m,![]() ),
),
若以E,C,P,F为顶点的四边形能构成平行四边形,
①以CE为边,∴CE∥PF,CE=PF,
∴F(m,![]() ),
),
∴![]() 或
或![]() ,
,
∴m1=1,m2=0(舍去),m3=![]() ,m4=
,m4=![]() ,
,
∴F1(1,![]() ),F2(
),F2(![]() ),F3(
),F3(![]() ),
),
②以CE为对角线,连接PF交CE于G,
∴CG=GE,PG=FG,
∴G(0,![]() ),
),
设P(m,![]() ),则F(m,
),则F(m,![]() ),
),
∴![]() ×(
×(![]() ,
,
∴m=1,m=0(舍去),
F4(1,0),
综上所述点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 或
或![]() .
.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则![]() (史称“皮克公式”).
(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
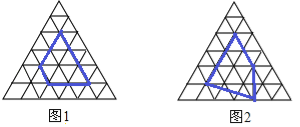
根据图中提供的信息填表:
格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
多边形1 | 8 | 1 | |
多边形2 | 7 | 3 | |
… | … | … | … |
一般格点多边形 | a | b | S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).