题目内容
 如图,将直角三角形ABO,∠ABO=90°,放入平面直角坐标系中,使OB边落在x轴上,将纸中AOB沿线段OA的垂直平分线MN对折,使O点落在点A的位置,B点落在B′的位置,若OB=1,∠BAO=30°,则点B′的坐标为
如图,将直角三角形ABO,∠ABO=90°,放入平面直角坐标系中,使OB边落在x轴上,将纸中AOB沿线段OA的垂直平分线MN对折,使O点落在点A的位置,B点落在B′的位置,若OB=1,∠BAO=30°,则点B′的坐标为考点:翻折变换(折叠问题),坐标与图形性质
专题:
分析:过B′点作B′C⊥AB于C.由折叠的性质可知,AB′=OB=1,∠B′AC=30°,在Rt△ABO中,根据三角函数可求AB,在Rt△AB′C中,根据三角函数可求CB′,AC,进一步得到点B′的坐标.
解答: 解:过B′点作B′C⊥AB于C.
解:过B′点作B′C⊥AB于C.
∵∠BAO=30°,
∴∠AOB=60°,
由折叠的性质可知,∠OAB=60°,AB′=OB=1,
∴∠B′AC=30°,
在Rt△ABO中,AB=OB•tan60°=
,
在Rt△AB′C中,CB′=AB′•sin30°=0.5,
AC=AB′•cos30°=0.5
,
∵1+0.5=1.5,
-0.5
=0.5
,
∴点B′的坐标为(1.5,0.5
).
故答案为:(1.5,0.5
).
 解:过B′点作B′C⊥AB于C.
解:过B′点作B′C⊥AB于C.∵∠BAO=30°,
∴∠AOB=60°,
由折叠的性质可知,∠OAB=60°,AB′=OB=1,
∴∠B′AC=30°,
在Rt△ABO中,AB=OB•tan60°=
| 3 |
在Rt△AB′C中,CB′=AB′•sin30°=0.5,
AC=AB′•cos30°=0.5
| 3 |
∵1+0.5=1.5,
| 3 |
| 3 |
| 3 |
∴点B′的坐标为(1.5,0.5
| 3 |
故答案为:(1.5,0.5
| 3 |
点评:考查了翻折变换(折叠问题),涉及的知识点有:折叠的性质,三角函数,以及坐标与图形性质,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为( )
| A、y=(x+1)2+4 |
| B、y=(x+1)2+2 |
| C、y=(x-1)2+4 |
| D、y=(x-1)2+2 |
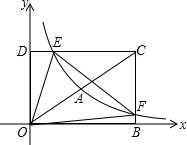 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y= 在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1300名学生一周的课外阅读时间不少于7小时的人数是
在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1300名学生一周的课外阅读时间不少于7小时的人数是 如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为
如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为