题目内容
如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )
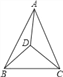
A. 100° B. 80° C. 70° D. 50°
练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
题目内容
如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )

A. 100° B. 80° C. 70° D. 50°
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案