题目内容
已知水平面上两个观测站A,B与C的距离都是100米,观测站A在C的北偏西50°,观测站B在C的南偏西10°.求AB距离是多少?
考点:解直角三角形的应用-方向角问题
专题:
分析:首先根据方向角的定义画出图形,连结AB,过C点作CD⊥AB于点D.在△ABC中,由等边对等角的性质及三角形内角和定理得出∠A=∠B=
(180°-∠ACB)=30°,根据等腰三角形三线合一的性质得出AB=2AD,然后解Rt△ADC,得出CD=
AC=50米,AD=
CD=50
米,所以AB=2AD=100
米.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答: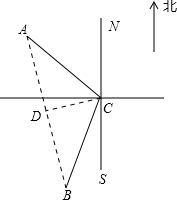 解:如图,连结AB,过C点作CD⊥AB于点D.
解:如图,连结AB,过C点作CD⊥AB于点D.
由题意AC=BC=100米,∠NCA=50°,∠SCB=10°,
在△ABC中,∵AC=BC,∠ACB=180°-∠NCA-∠SCB=120°,
∴∠A=∠B=
(180°-∠ACB)=30°.
∵AC=BC,CD⊥AB于点D,
∴AB=2AD.
在Rt△ADC中,∵∠ADC=90°,∠A=30°,AC=BC=100米,
∴CD=
AC=50米,AD=
CD=50
米,
∴AB=2AD=100
米.
 解:如图,连结AB,过C点作CD⊥AB于点D.
解:如图,连结AB,过C点作CD⊥AB于点D.由题意AC=BC=100米,∠NCA=50°,∠SCB=10°,
在△ABC中,∵AC=BC,∠ACB=180°-∠NCA-∠SCB=120°,
∴∠A=∠B=
| 1 |
| 2 |
∵AC=BC,CD⊥AB于点D,
∴AB=2AD.
在Rt△ADC中,∵∠ADC=90°,∠A=30°,AC=BC=100米,
∴CD=
| 1 |
| 2 |
| 3 |
| 3 |
∴AB=2AD=100
| 3 |
点评:本题考查了解直角三角形的应用-方向角问题,准确画出图形,作出适当的辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
在实数3.14,
,π,2.121121112…(两个2之间的1逐次加1个),
,
,
中,无理数的个数为( )
| 2 |
| 1 |
| 7 |
| 9 |
| 3 | 4 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,在⊙O中,OA⊥BC,∠CDA=50°,则∠AOC的度数为
如图,在⊙O中,OA⊥BC,∠CDA=50°,则∠AOC的度数为