题目内容
如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC、BD相交于点O，点E在AB上且BE=BO，则∠BEO=________度．
65
分析：因为AB=AD，∠BAD=80°，可求∠ABD=50°；又BE=BO，所以∠BEO=∠BOE，根据三角形内角和定理求解．
解答：∵ABCD是菱形，∴AB=AD．∴∠ABD=∠ADB．
∵∠BAD=80°，∴∠ABD=
×（180°-80°）=50°．
又∵BE=BO，
∴∠BEO=∠BOE=×（180°-50°）=65°．
故答案为：65．
点评：此题考查了菱形的性质和等腰三角形的性质以及三角形内角和定理．属基础题．
分析：因为AB=AD，∠BAD=80°，可求∠ABD=50°；又BE=BO，所以∠BEO=∠BOE，根据三角形内角和定理求解．
解答：∵ABCD是菱形，∴AB=AD．∴∠ABD=∠ADB．
∵∠BAD=80°，∴∠ABD=
×（180°-80°）=50°．又∵BE=BO，
∴∠BEO=∠BOE=
×（180°-50°）=65°．故答案为：65．
点评：此题考查了菱形的性质和等腰三角形的性质以及三角形内角和定理．属基础题．
练习册系列答案
相关题目
如图，已知菱形ABCD的边长为1.5cm，B，C两点在扇形AEF的
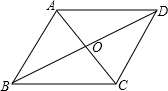如图，已知菱形ABCD的周长为16cm，∠ABC=60°，对角线AC和BD相交于点O，求AC和BD的长．
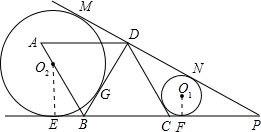上，半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N，半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G．
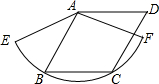如图，已知菱形ABCD为2cm．B、C两点在以点A为圆心的