题目内容
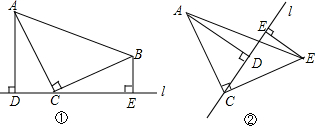 如图,在等腰直角三角形ABC中,∠ACB=90°,直线l过点C,AD⊥l,BE⊥l,垂足分别为D,E.
如图,在等腰直角三角形ABC中,∠ACB=90°,直线l过点C,AD⊥l,BE⊥l,垂足分别为D,E.
(1)试说明图①中△ACD≌△CBE;
(2)在图②中,△ACD与△CBE还全等吗?
解:(1)∵AD⊥l,BE⊥l,
∴∠ADC=∠BEC=90°,
∴∠DAC+∠ACD=90°,
又∵△ABC是等腰直角三角形,
∴AC=CB,
∵∠DAC、∠ECB都是∠ACD的余角,
∴∠DAC=∠ECB,
∵在△ACD和△CBE中,
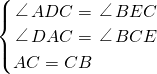 ,
,
∴△ACD≌△CBE(AAS).
(2)△ACD与△CBE还全等.
证明过程和(1)完全相同.
分析:(1)根据等角的余角相等,得出∠DAC=∠BCE,由△ABC是等腰直角三角形可得出CA=CB,利用AAS可证明①中△ACD≌△CBE;
(2)理由和(1)完全相同.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
∴∠ADC=∠BEC=90°,
∴∠DAC+∠ACD=90°,
又∵△ABC是等腰直角三角形,
∴AC=CB,
∵∠DAC、∠ECB都是∠ACD的余角,
∴∠DAC=∠ECB,
∵在△ACD和△CBE中,
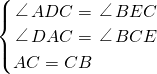 ,
,∴△ACD≌△CBE(AAS).
(2)△ACD与△CBE还全等.
证明过程和(1)完全相同.
分析:(1)根据等角的余角相等,得出∠DAC=∠BCE,由△ABC是等腰直角三角形可得出CA=CB,利用AAS可证明①中△ACD≌△CBE;
(2)理由和(1)完全相同.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:

(1)sad 的值为( ▼ )
的值为( ▼ )
(2)对于 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A=
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
 的值为( ▼ )
的值为( ▼ )A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( ▼ )
的值为( ▼ )
A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 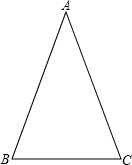 互唯一确定的.
互唯一确定的.
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
 的值为( ▼ )
的值为( ▼ ) B.
1 C.
B.
1 C.  D.
2
D.
2 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ . ,其中
,其中 为锐角,试求sad
为锐角,试求sad