题目内容
Rt△ABC中，∠C=90°，AC=8，BC=6，两等圆⊙A，⊙B外切，那么图中两个扇形（即阴影部分）的面积之和为
- A.
π - B.
π - C.
π - D.
π
A
分析：已知Rt△ABC中，∠ACB=90°，AC=8，BC=6，则根据勾股定理可知AB=10，两个扇形的面积的圆心角之和为90度，利用扇形面积公式即可求解．
解答：∵Rt△ABC中，∠ACB=90°，AC=8，BC=6，
∴AB=
=10，
∴S阴影部分=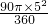
=
．
故选A．
点评：本题主要考查勾股定理的使用及扇形面积公式的灵活运用．
分析：已知Rt△ABC中，∠ACB=90°，AC=8，BC=6，则根据勾股定理可知AB=10，两个扇形的面积的圆心角之和为90度，利用扇形面积公式即可求解．
解答：∵Rt△ABC中，∠ACB=90°，AC=8，BC=6，
∴AB=
=10，∴S阴影部分=
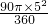=．故选A．
点评：本题主要考查勾股定理的使用及扇形面积公式的灵活运用．
练习册系列答案
相关题目
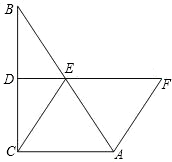延长线上，且AF=CE．求证：四边形ACEF是菱形．
如图，在Rt△ABC中，∠BAC=90°，点D、E、F分别是三边的中点，且CF=3cm，则DE=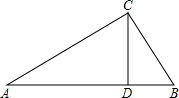
如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD=
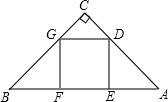点G在边BC上．
如图，Rt△ABC中，∠C=90°，D为AB的中点，DE⊥AB，AB=20，AC=12，则四边形ADEC的面积为