题目内容
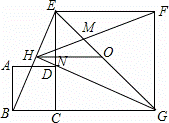
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①CH⊥BE;②HO
 BG;③S正方形ABCD:S正方形ECGF=1:
BG;③S正方形ABCD:S正方形ECGF=1: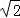 ;④EM:MG=1:(1+
;④EM:MG=1:(1+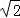 ),其中正确结论的序号为 .
),其中正确结论的序号为 .
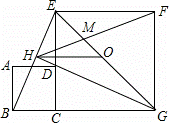
②解:∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°,
同理可得CE=CG,∠DCG=90°,
在△BCE和△DCG中,
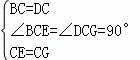 ,
,
∴△BCE≌△DCG,
∴∠BEC=∠DGC,
∵∠EDH=∠ CDG,∠DGC+∠CDG=90°,
CDG,∠DGC+∠CDG=90°,
∴∠EDH+∠BEC=90°,
∴∠EHD=90°,
∴HG⊥BE,则CH⊥BE错误,
则故①错误;
∵在△BGH和△EGH中,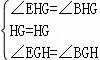 ,
,
∴△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中点,
∴HO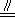
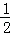 BG,
BG,
故②正确;
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
∵OH∥BC,
∴△DHN∽△DGC,
∴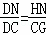 ,即
,即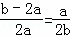 ,即a2+2ab﹣b2=0,
,即a2+2ab﹣b2=0,
解得:a=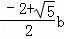 或a=
或a=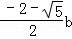 (舍去),
(舍去),
则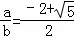 ,
,
则S正方形ABCD:S正方形ECGF=(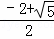 )2=
)2=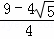 ,故③错误;
,故③错误;
∵EF∥OH,
∴△EFM∽△OMH,
∴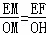 =
=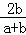 ,
,
∴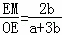 ,
,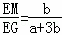
∴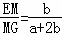 =
=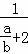 =
=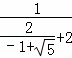 =
=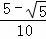 .故④错误.
.故④错误.
故正确的是②.
故答案是:②.

 阅读快车系列答案
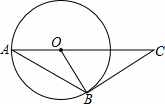
阅读快车系列答案如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
|
| A. | 70° | B. | 50° | C. | 45° | D. | 20° |
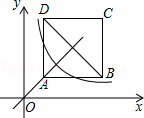
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y= 与正方形ABCD有公共点,则k的取值范围为( )
与正方形ABCD有公共点,则k的取值范围为( )
|
| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
计算(﹣3)+(﹣9)的结果是( )
|
| A. | ﹣12 | B. | ﹣6 | C. | +6 | D. | 12 |
不等式组 的整数解的个数是( )
的整数解的个数是( )
|
| A. | 3 | B. | 5 | C. | 7 | D. | 无数个 |

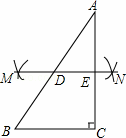
 AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;