题目内容
 (2013•邵阳)如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出
(2013•邵阳)如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出 | AB |
分析:根据垂径定理可得AF=
AB,再表示出AO、OF,然后利用勾股定理列式进行计算即可得解.
| 1 |
| 2 |
解答:解:∵弓形的跨度AB=3m,EF为弓形的高,
∴OE⊥AB,
∴AF=
AB=
m,
∵
所在圆O的半径为r,弓形的高EF=1m,
∴AO=r,OF=r-1,
在Rt△AOF中,AO2=AF2+OF2,
即r2=(
)2+(r-1)2,
解得r=
m.
答:
所在圆O的半径为
m.
∴OE⊥AB,
∴AF=
| 1 |
| 2 |
| 3 |
| 2 |
∵
 |
| AB |
∴AO=r,OF=r-1,
在Rt△AOF中,AO2=AF2+OF2,
即r2=(
| 3 |
| 2 |
解得r=
| 13 |
| 8 |
答:
 |
| AB |
| 13 |
| 8 |
点评:本题考查了垂径定理的应用,勾股定理的应用,此类题目通常采用把半弦,弦心距,半径三者放到同一个直角三角形中,利用勾股定理解答.

练习册系列答案
相关题目
 (2013•邵阳)如图是某班学生参加兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
(2013•邵阳)如图是某班学生参加兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( ) (2013•邵阳)如图是我市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )
(2013•邵阳)如图是我市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )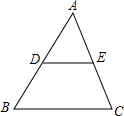 (2013•邵阳)如图所示,在△ABC中,点D、E分别是AB、AC的中点,连结DE,若DE=5,则BC=
(2013•邵阳)如图所示,在△ABC中,点D、E分别是AB、AC的中点,连结DE,若DE=5,则BC=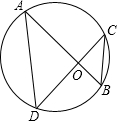 (2013•邵阳)如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是
(2013•邵阳)如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是 (2013•邵阳)如图所示,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件
(2013•邵阳)如图所示,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件