题目内容
 如图,AD=BC,AE=CF,AE⊥BD于E,CF⊥BD于F.求证:BE=DF.
如图,AD=BC,AE=CF,AE⊥BD于E,CF⊥BD于F.求证:BE=DF.考点:全等三角形的判定与性质
专题:证明题
分析:根据全等三角形的判定定理HL证得Rt△ADE≌Rt△CBF;然后由全等三角形的对应边相等可得DE=BF,进而即可证得结论.
解答:证明:∵AE⊥AD交BD于点E,CF⊥BC交BD于点F,
∴∠EAD=∠FCB=90°,
在Rt△ADE和Rt△CBF中,
,
∴Rt△ADE≌Rt△CBF(HL),
∴DE=BF,
∴BE=DF.
∴∠EAD=∠FCB=90°,
在Rt△ADE和Rt△CBF中,
|
∴Rt△ADE≌Rt△CBF(HL),
∴DE=BF,
∴BE=DF.
点评:本题考查了全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
多项式52x2-2x+1的次数是( )
| A、4 | B、3 | C、2 | D、1 |
以下列线段为边,不可能构成三角形的是( )
| A、101,102,103 |
| B、3,4,5 |
| C、5,7,12 |
| D、5,12,13 |

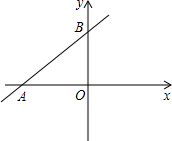 如图,在平面直角坐标系不,已知一次函数y=
如图,在平面直角坐标系不,已知一次函数y=