题目内容
9、如图所示，OB⊥OD，OC⊥OA，∠BOC=32°，那么∠AOD等于（ ）分析：根据两直线垂直，可得∠AOC=∠BOD=90°，由图示可得∠AOB=∠AOC-∠BOC，∠AOD=∠AOB+∠BOD，将∠BOC=32°代入即可求解．
解答：解：∵OB⊥OD，所以∠BOD=90°
∵OC⊥OA
∴∠AOC=90°
∴∠AOB=∠AOC-∠BOC=90°-32°=58°
∴∠AOD=∠AOB+∠BOD=90°+58°=148°
故选A．
∵OC⊥OA
∴∠AOC=90°
∴∠AOB=∠AOC-∠BOC=90°-32°=58°
∴∠AOD=∠AOB+∠BOD=90°+58°=148°
故选A．
点评：本题考查垂线的定义和角的运算，比较简单．
练习册系列答案
同步练习强化拓展系列答案
相关题目
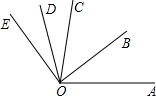如图所示，OB是∠AOC的平分线，OD是∠COE的平分线．
如图所示，OA=OD，OB=OC，请说明下列结论成立的理由：
