题目内容
18.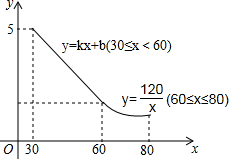 某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.
某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?
分析 (1)由图象知,当30≤x≤60时,图象过(60,2)和(30,5),运用待定系数法求解析式即可;
(2)根据销售产品的纯利润=销售量×单个利润,分30≤x≤60和60<x≤80列函数表达式;
(3)当30≤x≤60时,运用二次函数性质解决,当60<x≤80时,运用反比例函数性质解答.
解答 解:(1)当x=60时,y=$\frac{120}{60}$=2,
∴当30≤x≤60时,图象过(60,2)和(30,5),
设y=kx+b,则
$\left\{\begin{array}{l}{30k+b=5}\\{60k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-0.1}\\{b=8}\end{array}\right.$,
∴y=-0.1x+8(30≤x≤60);
(2)根据题意,当30≤x≤60时,W=(x-20)y-50=(x-20)(-0.1x+8)-50=-0.1x2+10x-210,
当60<x≤80时,W=(x-20)y-50=(x-20)•$\frac{120}{x}$-50=-$\frac{2400}{x}$+70,
综上所述:W=$\left\{\begin{array}{l}{-0.1{x}^{2}+10x-210(30≤x≤60)}\\{-\frac{2400}{x}+70(60<x≤80)}\end{array}\right.$;
(3)当30≤x≤60时,W=-0.1x2+10x-210=-0.1(x-50)2+40,
当x=50时,W最大=40(万元);
当60<x≤80时,W=-$\frac{2400}{x}$+70,
∵-2400<0,W随x的增大而增大,
∴当x=80时,W最大=-$\frac{2400}{80}$+70=40(万元),
答:当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元.
点评 本题主要考查了一次函数和二次函数的应用.分段讨论和数学建模是解决本题的关键所在.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
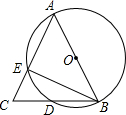 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的个数是( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的个数是( )
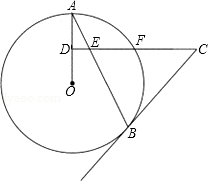 如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.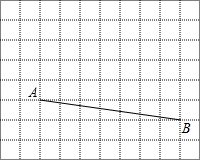 在10×8的网格中,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上.
在10×8的网格中,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上. 按要求解答:
按要求解答: 在图中作出点P,使得点P到C、D两点的距离相等,并且点P到OA、OB的距离也相等.(用尺规作图,保留作图痕迹,不写作法.)
在图中作出点P,使得点P到C、D两点的距离相等,并且点P到OA、OB的距离也相等.(用尺规作图,保留作图痕迹,不写作法.)