题目内容
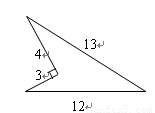
有一块田地的形状和尺寸如图所示,则它的面积为 .

考点:
勾股定理的应用..
专题:
应用题.
分析:
连接AB,则在直角△ABC中,已知AC,BC可以求AB,根据AB,BD,AD可以判定△ABD为直角三角形,且四边形ABCD的面积S=S△ABD﹣S△ABC.所以求直角△ABC和直角△ABD的面积即可.
解答:
解:连接AB,
在直角△ABC中,AC=4,BC=3,
则AB=![]() =5,
=5,
又∵AB2+BD2=25+144=169=AD2,
∴△ABD为直角三角形,
且四边形ABCD的面积为S=S△ABD﹣S△ABC,
=![]() ×AB×BD﹣
×AB×BD﹣![]() ×AC×BC,
×AC×BC,
=![]() ×12×5﹣
×12×5﹣![]() ×3×4,
×3×4,
=30﹣6,
=24.
故答案为:24.

点评:
本题考查了勾股定理在实际生活中的运用,考查了直角三角形的判定,本题中连接AB分别计算AB、S△ABD、S△ABC是解题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图,有一块田地的形状和尺寸如图所示,则它的面积为
如图,有一块田地的形状和尺寸如图所示,则它的面积为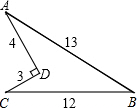 有一块田地的形状和尺寸如图所示,求它的面积.
有一块田地的形状和尺寸如图所示,求它的面积. 有一块田地的形状和尺寸如图所示,则它的面积为
有一块田地的形状和尺寸如图所示,则它的面积为 有一块田地的形状和尺寸如图所示∠B=∠D=90°,∠A=60°,AB=5米,AD=4米,试求它的面积.
有一块田地的形状和尺寸如图所示∠B=∠D=90°,∠A=60°,AB=5米,AD=4米,试求它的面积.