Question

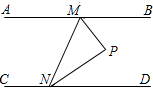（2013•晋江市质检）如图，动点M、N分别在直线AB与CD上，且AB∥CD，∠BMN与∠MND的角平分线相交于点P，若以MN为直径作⊙O，则点P与⊙O的位置关系是（　　）

A．点P在⊙O外

B．点P在⊙O内

C．点P在⊙O上

D．以上都有可能

Answer 1

分析：先根据平行线的性质得出∠BMN+∠MND=180°，再由角平分线的性质可得出∠PMN=

1

2

∠BMN，∠PNM=

1

2

∠MND，故可知∠PMN+∠PNM=90°，由三角形的内角和是180°得出∠MPN=90°，再由直角三角形斜边上的中线等于斜边的一半得出OP=

1

2

MN，进而根据点与圆的位置关系即可得出结论．

解答：解：∵AB∥CD，
∴∠BMN+∠MND=180°，
∵∠BMN与∠MND的平分线相交于点P，
∴∠PMN=

1

2

∠BMN，∠PNM=

1

2

∠MND，
∴∠PMN+∠PNM=90°，
∴∠MPN=180°-（∠PMN+∠PNM）=180°-90°=90°，
∴以MN为直径作⊙O时，OP=

1

2

MN=⊙O的半径，
∴点P在⊙O上．
故选C．

点评：本题考查的是平行线的性质、角平分线的定义、三角形内角和定理、直角三角形的性质及点与圆的位置关系，根据条件得到OP=

1

2

MN是解题的关键．