题目内容

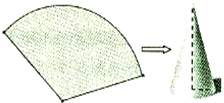
如图，半径为2的圆形纸片，沿半径OA、OB裁成1：3两部分，用得到的扇形围成圆锥的侧面，则圆锥的底面半径分别为______．
如图，分两种情况，
①设扇形S2做成圆锥的底面半径为R2，
由题意知：扇形S2的圆心角为270度，
则它的弧长=
270π×2
180
=2πR2，R2=
3
2
；

②设扇形S1做成圆锥的底面半径为R1，
由题意知：扇形S1的圆心角为90度，
则它的弧长=
90π×2
180
=2πR1，R1=
1
2
．
故答案为
3
2
或
1
2
．
练习册系列答案
相关题目
如图，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE、CF交于点G，半径BE、CD交于点H，且点C是
AB
的中点，若扇形的半径为2，则图中阴影部分的面积等于______．
如图，在△ABC中，∠C=90°，AC=BC，AB=2
2
，点O为AB的中点，以点O为圆心作半圆与边AC相切于点D．则图中阴影部分的面积为（　　）
A．1-
1
4
π		B．1-
1
8
π		C．2-
3
4
π		D．2-
1
4
π
如图所示，在⊙O中，
AD
=
AC
，弦AB与弦AC交于点A，弦CD与AB交于点F，连接BC．
（1）求证：AC2=AB•AF；
（2）若⊙O的半径长为2cm，∠B=60°，求图中阴影部分面积．
把半径为r的圆铁片沿着半径OA、OB剪成面积比为1：2的两个扇形S1、S2（如图），把这两个围成两个无底的圆锥．设这两个圆锥的高分别为h1、h2，则h1与h2的大小比较是（　　）
A．h1＞h2B．h1＜h2C．h1=h2D．不能确定
用圆心角为120°，半径为6cm的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的高是（　　）
A．
2
cm		B．3
2
cm		C．4
2
cm		D．4cm
王芳制作了一个圆锥形纸帽，其尺寸如图．则将这个纸帽展开成扇形时的圆心角等于（　　）
A．45°B．60°C．90°D．120°
如图，一个直角三角形纸板，其两条直角边长分别为6cm和8cm，小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体．请你帮小明推算出这个旋转体的全面积．（π取3.14）
四位好朋友在一次聚会上，他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口饮料杯，如图所示，盛满饮料后他们约定：先各自饮去杯中饮料的一半．设剩余饮料的高度从左到右依次为h1，h2，h3，h4，则它们之间有以下的大小关系（　　）
A．h2＞h1＞h4B．h1＞h2＞h3C．h3＞h2＞h4D．h2＞h4＞h1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网