题目内容
 如图,一次函数
如图,一次函数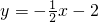 的图象分别交x轴、y轴于A,B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数
的图象分别交x轴、y轴于A,B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数 (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.
(1)A点坐标为______,B点坐标为______;
(2)求反比例函数的表达式;
(3)连接OP、AQ,求证:四边形APOQ是菱形.
(1)解:对于y=- x-2,令y=0,则-
x-2,令y=0,则- x-2=0,解得x=-4,∴A点坐标为(-4,0);
x-2=0,解得x=-4,∴A点坐标为(-4,0);
令x=0,则y=-2,所以B点坐标为(0,-2);
故答案为(-4,0);(0,-2);
(2)解:∵P为AB的中点,PC⊥x轴,
∴C为OA的中点,即OC= OA=2,
OA=2,
∴C点坐标为(-2,0),
又∵tan∠AOQ= ,
,
∴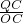 =
= ,
,
∴QC=1,
∴Q点的坐标为(-2,1),
把Q(-2,1)代入y= 得k=-2,
得k=-2,
∴反比例函数的表达式为y=- ;
;
(3)证明:∵C点坐标为(-2,0),
把x=-2代入y=- x-2得y=-1,
x-2得y=-1,
∴P点坐标为(-2,-1),
而Q点的坐标为(-2,1),
∴点Q与点P关于x轴对称,
∴CQ=CP,
又∵OC=AC,OA⊥PQ,
∴四边形APOQ是菱形.
分析:(1)根据坐标轴上点的坐标易得A点坐标为(-4,0);B点坐标为(0,-2);
(2)由P为AB的中点,PC⊥x轴,易得OC= OA=2和C点坐标为(-2,0),再根据正切的定义得到
OA=2和C点坐标为(-2,0),再根据正切的定义得到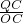 =
= ,则QC=1,可确定Q点的坐标为(-2,1),然后把Q(-2,1)代入y=
,则QC=1,可确定Q点的坐标为(-2,1),然后把Q(-2,1)代入y= 即可求出k的值;
即可求出k的值;
(3)先确定P点坐标(-2,-1),则点Q与点P关于x轴对称,即CQ=CP,又∵OC=AC,OA⊥PQ,根据对角线互相垂直平分的四边形为菱形即可得到结论.
点评:本题考查了反比例函数的综合题:先根据几何条件确定某些点的坐标,然后利用待定系数法确定反比例函数的解析式,再运用反比例函数的性质解决问题.也考查了菱形的判定.
 x-2,令y=0,则-
x-2,令y=0,则- x-2=0,解得x=-4,∴A点坐标为(-4,0);
x-2=0,解得x=-4,∴A点坐标为(-4,0);令x=0,则y=-2,所以B点坐标为(0,-2);
故答案为(-4,0);(0,-2);
(2)解:∵P为AB的中点,PC⊥x轴,
∴C为OA的中点,即OC=
 OA=2,
OA=2,∴C点坐标为(-2,0),
又∵tan∠AOQ=
 ,
,∴
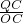 =
= ,
,∴QC=1,
∴Q点的坐标为(-2,1),
把Q(-2,1)代入y=
 得k=-2,
得k=-2,∴反比例函数的表达式为y=-
 ;
;(3)证明:∵C点坐标为(-2,0),
把x=-2代入y=-
 x-2得y=-1,
x-2得y=-1,∴P点坐标为(-2,-1),
而Q点的坐标为(-2,1),
∴点Q与点P关于x轴对称,
∴CQ=CP,
又∵OC=AC,OA⊥PQ,
∴四边形APOQ是菱形.
分析:(1)根据坐标轴上点的坐标易得A点坐标为(-4,0);B点坐标为(0,-2);
(2)由P为AB的中点,PC⊥x轴,易得OC=
 OA=2和C点坐标为(-2,0),再根据正切的定义得到
OA=2和C点坐标为(-2,0),再根据正切的定义得到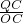 =
= ,则QC=1,可确定Q点的坐标为(-2,1),然后把Q(-2,1)代入y=
,则QC=1,可确定Q点的坐标为(-2,1),然后把Q(-2,1)代入y= 即可求出k的值;
即可求出k的值;(3)先确定P点坐标(-2,-1),则点Q与点P关于x轴对称,即CQ=CP,又∵OC=AC,OA⊥PQ,根据对角线互相垂直平分的四边形为菱形即可得到结论.
点评:本题考查了反比例函数的综合题:先根据几何条件确定某些点的坐标,然后利用待定系数法确定反比例函数的解析式,再运用反比例函数的性质解决问题.也考查了菱形的判定.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图,已知反比例函数y=
如图,已知反比例函数y=
 解答:
解答:
