题目内容
若点A(8,y1)、B(2,y2)在双曲线 上,则y1和y2的大小关系为________.
上,则y1和y2的大小关系为________.
y1<y2
分析:根据反比例函数图象上点的坐标特征,将点A(8,y1)、B(2,y2)分别代入双曲线 ,求得y1和y2的值,然后再来比较它们的大小.
,求得y1和y2的值,然后再来比较它们的大小.
解答:∵点A(8,y1)、B(2,y2)在双曲线 上,
上,
∴y1=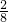 =
= ,y2=
,y2= =1;
=1;
∵ <1,
<1,
∴y1<y2.
故答案是:y1<y2
点评:此题主要考查了反比例函数图象上点的坐标特征.解答此题时,也可以利用反比例函数图象的单调性来解决问题.
分析:根据反比例函数图象上点的坐标特征,将点A(8,y1)、B(2,y2)分别代入双曲线
 ,求得y1和y2的值,然后再来比较它们的大小.
,求得y1和y2的值,然后再来比较它们的大小.解答:∵点A(8,y1)、B(2,y2)在双曲线
 上,
上,∴y1=
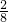 =
= ,y2=
,y2= =1;
=1;∵
 <1,
<1,∴y1<y2.
故答案是:y1<y2
点评:此题主要考查了反比例函数图象上点的坐标特征.解答此题时,也可以利用反比例函数图象的单调性来解决问题.

练习册系列答案
相关题目
若点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数y=-
的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是( )
| 2 |
| x |
| A、y1<y3<y2 |
| B、y2<y3<y3 |
| C、y1<y2<y3 |
| D、y2<y3<y1 |