题目内容
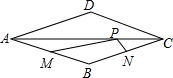菱形ABCD的两条对角线的长分别为6和8，点M、N分别是边AB、BC的中点，点P是对角线AC上的一个动A点，则PM+PN的最小值是________．
5
分析：要求PM+PN的最小值，PM，PN不能直接求，可考虑通过作辅助线转化PN，PM的值，从而找出其最小值求解．
解答：
解：如图：
作ME⊥AC交AD于E，连接EN，
则EN就是PM+PN的最小值，
∵M、N分别是AB、BC的中点，
∴BN=BM=AM，
∵ME⊥AC交AD于E，
∴AE=AM，
∴AE=BN，AE∥BN，
∴四边形ABNE是平行四边形，
∴EN
AB，
而由已知可得AB=
=5，
∴PM+PN的最小值为5，
故答案为5．
点评：本题考了查菱形的性质和轴对称及平行四边形的判定等知识的综合应用．综合运用这些知识是解决本题的关键．
分析：要求PM+PN的最小值，PM，PN不能直接求，可考虑通过作辅助线转化PN，PM的值，从而找出其最小值求解．
解答：
解：如图：作ME⊥AC交AD于E，连接EN，
则EN就是PM+PN的最小值，
∵M、N分别是AB、BC的中点，
∴BN=BM=AM，
∵ME⊥AC交AD于E，
∴AE=AM，
∴AE=BN，AE∥BN，
∴四边形ABNE是平行四边形，
∴EN
AB，而由已知可得AB=
=5，∴PM+PN的最小值为5，
故答案为5．
点评：本题考了查菱形的性质和轴对称及平行四边形的判定等知识的综合应用．综合运用这些知识是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
）。
）。