题目内容
如图，从A地到B地有两条路可走，一条路是大半圆，另一条路是4个小半圆．有一天，一只猫和一只老鼠同时从A地到B地．老鼠见猫沿着大半圆行走，它不敢与猫同行（怕被猫吃掉），就沿着4个小半圆行走．假设猫和老鼠行走的速度相同，那么下列结论正确的是
- A.猫先到达B地
- B.老鼠先到达B地
- C.猫和老鼠同时到达B地
- D.无法确定
C
分析：利用半圆的弧长公式，即可分别求得两个路径的长，然后进行比较即可．
解答：以AB为直径的半圆的长是：
π•AB；
设四个小半圆的直径分别是a，b，c，d，则a+b+c+d=AB．
则老鼠行走的路径长是：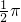
a+πb+πc+πd=π（a+b+c+d）=π•AB．
故猫和老鼠行走的路径长相同．
故选C．
点评：本题考查了半圆的弧长公式，正确理解a+b+c+d=AB是关键．
分析：利用半圆的弧长公式，即可分别求得两个路径的长，然后进行比较即可．
解答：以AB为直径的半圆的长是：
π•AB；设四个小半圆的直径分别是a，b，c，d，则a+b+c+d=AB．
则老鼠行走的路径长是：
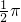a+πb+πc+πd=π（a+b+c+d）=π•AB．故猫和老鼠行走的路径长相同．
故选C．
点评：本题考查了半圆的弧长公式，正确理解a+b+c+d=AB是关键．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
20、如图，从A地到B地有多条道路，一般地，人们会走中间的直路，而不会走其他的曲折的路，这是因为（ ）
16、如图，从A地到B地有3条路线可供选择，从B地到C地有2条路线可供选择，则从A地到C地可供选择的方案有
20、如图，从A地到B地有多条路，人们常会走第③条路，而不会走曲折的路，理由是（ ）
如图，从A地到B地有两条路可走，一条路是大半圆，另一条路是4个小半圆．有一天，一只猫和一只老鼠同时从A地到B地．老鼠见猫沿着大半圆行走，它不敢与猫同行（怕被猫吃掉），就沿着4个小半圆行走．假设猫和老鼠行走的速度相同，那么下列结论正确的是（ ）
如图，从A地到B地有多条路径可通达，一条公路决定沿图中实线路径修筑，其依据是