题目内容
 如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是
如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是
- A.①②
- B.①②③
- C.①②④
- D.①②③④
B
分析:大正方形的面积是49,则其边长是7,显然,利用勾股定理可得①x2+y2=49;
小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即②x-y=2;
还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即4× xy+4=49,化简得③2xy+4=49;
xy+4=49,化简得③2xy+4=49;
其中④x+y=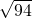 ,故不成立.
,故不成立.
解答:①大正方形的面积是49,则其边长是7,显然,利用勾股定理可得x2+y2=49,故选项①正确;
②小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即x-y=2,故选项②正确;
③根据图形可得四个三角形的面积+小正方形的面积=大正方形的面积,即4× xy+4=49,化简得2xy+4=49,故选项③正确;
xy+4=49,化简得2xy+4=49,故选项③正确;
④ ,则x+y=
,则x+y=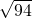 ,故此选项不正确.
,故此选项不正确.
故选B.
点评:本题利用了勾股定理、面积分割法等知识.
分析:大正方形的面积是49,则其边长是7,显然,利用勾股定理可得①x2+y2=49;
小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即②x-y=2;
还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即4×
 xy+4=49,化简得③2xy+4=49;
xy+4=49,化简得③2xy+4=49;其中④x+y=
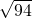 ,故不成立.
,故不成立.解答:①大正方形的面积是49,则其边长是7,显然,利用勾股定理可得x2+y2=49,故选项①正确;
②小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即x-y=2,故选项②正确;
③根据图形可得四个三角形的面积+小正方形的面积=大正方形的面积,即4×
 xy+4=49,化简得2xy+4=49,故选项③正确;
xy+4=49,化简得2xy+4=49,故选项③正确;④
 ,则x+y=
,则x+y=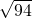 ,故此选项不正确.
,故此选项不正确.故选B.
点评:本题利用了勾股定理、面积分割法等知识.

练习册系列答案
相关题目
 如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( ) 如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有
如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有

