Question

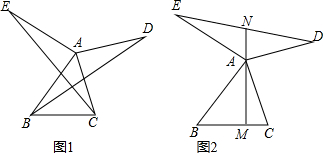如图1，AB=AE，AC=AD，∠BAE=∠CAD=90°．
（1）证明：EC=BD；
（2）证明：EC⊥BD；
（3）如图2，连接ED，若N点为DE的中点，连接NA并延长与BC交于点M，证明：AM⊥BC．

Answer 1

考点：全等三角形的判定与性质

专题：证明题

分析：（1）求出∠CAE=∠BAD，证出△BAD≌△EAC即可；
（2）根据△BAD≌△EAC，推出∠D=∠ACE，根据∠D+∠AMD=90°求出∠ACE+∠CMO=90°，求出∠COM=90°即可；
（3）延长AN到H，使NH=AN，连接EH、DH，求出四边形ADHE是平行四边形，推出∠DHN=∠EAH，AE=DH=AB，求出∠ADH=∠BAC，证△ADH≌△ACB，推出∠AHD=∠B，求出∠B+∠BAM=90°即可．

解答：证明：（1）∵∠BAE=∠CAD=90°，
∴∠BAE+∠BAC=∠CAD+∠BAC，
∴∠CAE=∠BAD，
在△BAD和△EAC中，

BA=AE ∠BAD=∠EAC AD=AC

，
∴△BAD≌△EAC（SAS），
∴EC=BD；

（2）∵△BAD≌△EAC，
∴∠D=∠ACE，
∵∠DAC=90°，
∴∠D+∠AMD=90°，
∵∠AMD=∠CMO，
∴∠ACE+∠CMO=90°，
∴∠COM=90°，
∴EC⊥BD；


（3）延长AN到H，使NH=AN，连接EH、DH，
∵N为DE中点，
∴四边形ADHE是平行四边形，
∴∠DHN=∠EAH，AE=DH=AB，
∵∠EAD+∠BAC=180°，∠EAD+∠ADH=180°，
∴∠ADH=∠BAC，
在△ADH和△ACB中，

AD=AC ∠ADH=∠BAC DH=AB

，
∴△ADH≌△ACB（SAS），
∴∠AHD=∠B，
∵N、A、M是一条直线，
∴∠EAH+∠BAM=90°，
∴∠B+∠BAM=90°，
∴MN⊥BC．

点评：本题考查了全等三角形的性质和判定，平行四边形的性质和判定，三角形内角和定理的应用，题目比较典型，有一定的难度．