题目内容
等腰直角三角形ABC中，∠A=90°，⊙O为△ABC的内切圆，D、E、F分别为切点，则
=
- A.
- B.
- C.
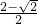
- D.
C
分析：由题意可知AE=AF，BD=BE，CD=CF，△AEF为等腰直角三角形，推出△AEF∽△ABC，然后，设AB=AC=a，根据相似三角形的性质，即可推出结论．
解答：∵⊙O为△ABC的内切圆，
∴AE=AF，BD=BE，CD=CF，
∵等腰直角三角形ABC中，∠A=90°，
∴BD=DC，△AEF为等腰直角三角形，
∴△AEF∽△ABC，
设AB=AC=a，
∴BC=
a，
∴BD=CD=BE=CF=
a，
∴AE=AF=a-a，
∴EF：BC=AF：AC=（2-）：2．
故选择C．
点评：本题主要考查相似三角形的判定和性质、三角形内切圆的性质，关键在于求证△AEF∽△ABC．
分析：由题意可知AE=AF，BD=BE，CD=CF，△AEF为等腰直角三角形，推出△AEF∽△ABC，然后，设AB=AC=a，根据相似三角形的性质，即可推出结论．
解答：∵⊙O为△ABC的内切圆，
∴AE=AF，BD=BE，CD=CF，
∵等腰直角三角形ABC中，∠A=90°，
∴BD=DC，△AEF为等腰直角三角形，
∴△AEF∽△ABC，
设AB=AC=a，
∴BC=
a，∴BD=CD=BE=CF=
a，∴AE=AF=a-
a，∴EF：BC=AF：AC=（2-
）：2．故选择C．
点评：本题主要考查相似三角形的判定和性质、三角形内切圆的性质，关键在于求证△AEF∽△ABC．
练习册系列答案
相关题目
把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点逆时针旋转（旋转角α满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图②）．
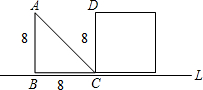AB与CD重合．设x秒时，三角形与正方形不重叠部分的面积为ym2．
如图，等腰直角三角形△ABC中，∠ACB=90°，点D是BC的中点，CE⊥AD于点F交AB于点E，CH是AB上的高交AD于点G．