题目内容
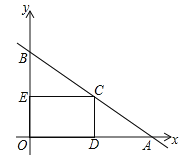
【题目】在平面直角坐标系中，直线AB与x轴、y轴分别交于A（6，0），B（0，3）两点．点C为线段AB上的一个动点，过点C作CD⊥x轴于点D，作CE⊥y轴与点E，求矩形OECD的最大面积，并求此时点C的坐标．
【答案】矩形面积最大
，此时C（3，
）．
【解析】
直接利用已知求出直线AB的解析式，进而得出S矩形OECD＝CDCE＝|m||
m+3|
m2+3m，配方即可得出答案．
∵直线AB与x轴、y轴分别交于A（6，0），B（0，3）两点，∴设直线AB解析式为：y＝kx+3，∴6k+3＝0，解得：k，∴直线AB解析式为：yx+3；
设点C（m，m+3），其中m＞0，S矩形OECD＝CDCE＝|m||m+3|m2+3m=（m﹣3）2
，当m＝3时，矩形面积最大，此时C（3，）．
练习册系列答案
阅读快车系列答案
相关题目
