题目内容
点E是矩形ABCD边CD所在直线上一点,且DE=| 1 | 3 |
分析:由DE、CD的比例关系,易求得DE的长,然后分两种情况考虑:
①E点在线段CD上,设折线为M、N,首先在Rt△ADE中,利用勾股定理求得PE的长,设折线MN与PE的交点为O,那么在Rt△PON中,可求得ON的值;然后延长PE交AD的延长线于F,根据△MOF∽△NOB来求得MO的值,从而由OM+ON得到折痕MN的长;
②E点在线段CD的延长线上,解法同上.
①E点在线段CD上,设折线为M、N,首先在Rt△ADE中,利用勾股定理求得PE的长,设折线MN与PE的交点为O,那么在Rt△PON中,可求得ON的值;然后延长PE交AD的延长线于F,根据△MOF∽△NOB来求得MO的值,从而由OM+ON得到折痕MN的长;
②E点在线段CD的延长线上,解法同上.
解答: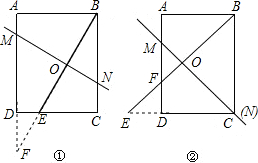 解:如图;
解:如图;
由题意知:DE=
CD=1;
①当E点在线段CD上时,DE=1,CE=2;
在Rt△BCE中,由勾股定理得:
BE=
=2
;
由于折痕MN垂直平分BE,则OB=OE=
;
在Rt△BON中,ON=OB•tan∠EBC=
OB=
;
延长BE至F,则DF=2DE=2,EF=
;
易知:△BON∽△FOM,则:
=
,即
=
,故OM=2ON;
∴MN=3ON=
;
②当点E在线段CD的延长线上时,DE=1,CE=4;
此时△BCE是等腰直角三角形,故N、C重合;
易得:BO=ON=OE=2
;
在Rt△DEF中,∠E=45°,则DF=DE=1,EF=
;
∴OF=OE-EF=
;
同①可得:
=
=
,即ON=2OM,
∴MN=
ON=3
;
综上可知:折痕MN的长为:
或3
.
 解:如图;
解:如图;由题意知:DE=
| 1 |
| 3 |
①当E点在线段CD上时,DE=1,CE=2;
在Rt△BCE中,由勾股定理得:
BE=
| BC2+CE2 |
| 5 |
由于折痕MN垂直平分BE,则OB=OE=
| 5 |
在Rt△BON中,ON=OB•tan∠EBC=
| 1 |
| 2 |
| ||
| 2 |
延长BE至F,则DF=2DE=2,EF=
| 5 |
易知:△BON∽△FOM,则:
| OB |
| OF |
| ON |
| OM |
| ||
2
|
| ON |
| OM |
∴MN=3ON=
3
| ||
| 2 |
②当点E在线段CD的延长线上时,DE=1,CE=4;
此时△BCE是等腰直角三角形,故N、C重合;
易得:BO=ON=OE=2
| 2 |
在Rt△DEF中,∠E=45°,则DF=DE=1,EF=
| 2 |
∴OF=OE-EF=
| 2 |
同①可得:
| ON |
| OM |
| OB |
| OF |
2
| ||
|
∴MN=
| 3 |
| 2 |
| 2 |
综上可知:折痕MN的长为:
3
| ||
| 2 |
| 2 |
点评:此题主要考查了图形的翻折变换、勾股定理以及相似三角形的判定和性质等知识,由于E点的位置不确定,因此要注意分类讨论思想的运用,以免漏解.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
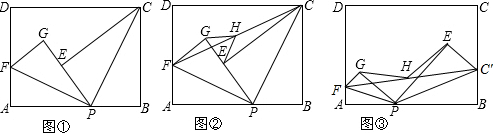
 如图:点P是矩形ABCD边AB上的一点,AB=6,BC=8,BP=2AP,Q是AD边上的一点,当AQ等于多少时,△PAQ∽△PBC.
如图:点P是矩形ABCD边AB上的一点,AB=6,BC=8,BP=2AP,Q是AD边上的一点,当AQ等于多少时,△PAQ∽△PBC.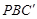 沿
沿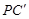 翻折得到△
翻折得到△ ,连接
,连接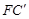 ,取
,取