题目内容
9.为了测量学校旗杆的高度,身高相同的小张和小李站在操场如图所示的位置,小张在C处测得旗杆顶端的仰角为18°,小李在D处测得旗杆顶端的仰角为72°,又已知两人之间的距离CD为24米,两人的眼睛离地面的距离AC、BD均为1.6米,旗杆的底部N距离操场所在平面的垂直高度NK=2米,求旗杆MN的高度.(参考数据:tan18°≈$\frac{1}{3}$.)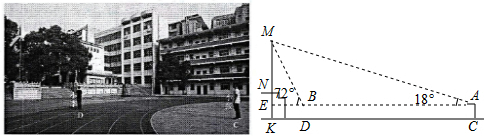
分析 设ME=x,通过解直角△EBM得到ME的长度,通过解直角△AME得到ME的长度,由此列出方程求得x的值,然后结合图形找到相关线段的和差关系进行解答.
解答 解:设ME=x.
∵在直角△AME中,∠MAE=18°,
∴EM=AE•tan18°=$\frac{1}{3}$AE.即AE=3x;
∵在直角△EBM中,∠MBE=72°,
∴ME=BEtan72°=3BE,即BE=$\frac{1}{3}$ME,
∴3x-$\frac{1}{3}$x=24,
解得x=9,
∴MK=10.6米,
又NK=2米,
∴MN=10.6-2=8.6(米).
答:旗杆MN的高度是8.6米.
点评 本题考查解直角三角形的应用-仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
19.下列标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
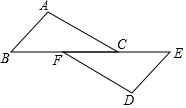 如图,AB=DE,AC=DF,BF=CE;若∠B=50°,∠D=100°,则∠EFD=30°.
如图,AB=DE,AC=DF,BF=CE;若∠B=50°,∠D=100°,则∠EFD=30°.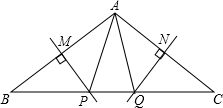 如图所示,MP和 NQ分别垂直平分AB 和AC.
如图所示,MP和 NQ分别垂直平分AB 和AC.
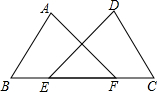 如图,点E、F在线段BC上且F在E的右侧,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
如图,点E、F在线段BC上且F在E的右侧,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.