题目内容
已知△ABC内接于⊙O,AB=AC,半径OB=5cm,圆心O到BC的距离为3cm,则AB的长为________cm.
4 或2
或2
分析:此题分情况考虑:当三角形的外心在三角形的内部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长;当三角形的外心在三角形的外部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长.
解答: 解:如图,当三角形的外心在三角形的内部时,
解:如图,当三角形的外心在三角形的内部时,
连接AO并延长到BC于点D,
∵AB=AC,O为外心,
∴AD⊥BC,
在直角三角形BOD中,根据勾股定理,得BD=4.
在直角三角形ABD中,根据勾股定理,得AB=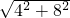 =4
=4 (cm);
(cm);
当三角形的外心在三角形的外部时,
在直角三角形BOD中,根据勾股定理,得BD=4.
在直角三角形ABD中,根据勾股定理,得AB= =2
=2 (cm).
(cm).
故答案为:4 或2
或2 .
.
点评:此题主要是勾股定理的运用.注意:三角形的外心可能在三角形的外部,可能在三角形的内部,也可能在三角形的一边上,即直角三角形的外心在其斜边的中点.
 或2
或2
分析:此题分情况考虑:当三角形的外心在三角形的内部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长;当三角形的外心在三角形的外部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长.
解答:
 解:如图,当三角形的外心在三角形的内部时,
解:如图,当三角形的外心在三角形的内部时,连接AO并延长到BC于点D,
∵AB=AC,O为外心,
∴AD⊥BC,
在直角三角形BOD中,根据勾股定理,得BD=4.
在直角三角形ABD中,根据勾股定理,得AB=
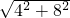 =4
=4 (cm);
(cm);当三角形的外心在三角形的外部时,
在直角三角形BOD中,根据勾股定理,得BD=4.
在直角三角形ABD中,根据勾股定理,得AB=
 =2
=2 (cm).
(cm).故答案为:4
 或2
或2 .
.点评:此题主要是勾股定理的运用.注意:三角形的外心可能在三角形的外部,可能在三角形的内部,也可能在三角形的一边上,即直角三角形的外心在其斜边的中点.

练习册系列答案
相关题目
 如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.
如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E. 终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
 (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. (2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=
(2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=