题目内容
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:
①当m=﹣3时,函数图象的顶点坐标是(
 ,
,
 );
);
②当m>0时,函数图象截x轴所得的线段长度大于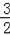
 ;
;
③当m<0时,函数在x>
 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④ B.①②④ C.①③④ D.②④
B【考点】二次函数的性质.
【专题】压轴题;新定义.
【分析】①当m=﹣3时,根据函数式的对应值,可直接求顶点坐标;②当m>0时,直接求出图象与x轴两交点坐标,再求函数图象截x轴所得的线段长度,进行判断;③当m<0时,根据对称轴公式,进行判断;④当m≠0时,函数图象经过同一个点.
【解答】解:根据定义可得函数y=2mx2+(1﹣m)x+(﹣1﹣m),
①当m=﹣3时,函数解析式为y=﹣6x2+4x+2,
∴
 =﹣
=﹣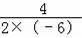
 =
=
 ,
,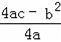
 =
=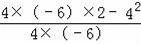
 =
=
 ,
,
∴顶点坐标是(
 ,
,
 ),正确;
),正确;
②函数y=2mx2+(1﹣m)x+(﹣1﹣m)与x轴两交点坐标为(1,0),(﹣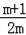
 ,0),
,0),
当m>0时,1﹣(﹣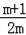
 )=
)=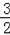
 +
+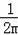
 >
>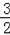
 ,正确;
,正确;
③当m<0时,函数y=2mx2+(1﹣m)x+(﹣1﹣m)开口向下,对称轴x=
 ﹣
﹣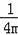
 >
>
 ,
,
∴x可能在对称轴左侧也可能在对称轴右侧,错误;
④y=2mx2+(1﹣m)x+(﹣1﹣m)=m(2x2﹣x﹣1)+x﹣1,若使函数图象恒经过一点,m≠0时,应使2x2﹣x﹣1=0,可得x1=1,x2=﹣
 ,当x=1时,y=0,当x=﹣
,当x=1时,y=0,当x=﹣
 时,y=﹣
时,y=﹣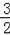
 ,则函数一定经过点(1,0)和(﹣
,则函数一定经过点(1,0)和(﹣
 ,﹣
,﹣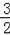
 ),正确.
),正确.
故选B.
【点评】公式法:y=ax2+bx+c的顶点坐标为(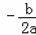
 ,
,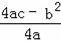
 ),对称轴是x=
),对称轴是x=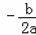
 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 有意义.
有意义.


 C.
C.