题目内容
(1)把两个含有45°角的直角三角板如图1放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.求证:AF⊥BE.(2)把两个含有30°角的直角三角板如图2放置,点
 D在BC上,连接BE,AD,AD的延长线交BE于点F.问AF与BE是否垂直?并说明理由.
D在BC上,连接BE,AD,AD的延长线交BE于点F.问AF与BE是否垂直?并说明理由.
分析:(1)图1,图2是两组不同类别的直角三角形,图1可考虑证明△ACD≌△BCE,利用对应角相等推出互余关系,证明垂直.
(2)图2可考虑证明相似三角形,同样有对应角相等,利用相等角推出互余关系,证明垂直.
(2)图2可考虑证明相似三角形,同样有对应角相等,利用相等角推出互余关系,证明垂直.
解答:(1)证明:在△ACD和△BCE中,AC=BC,∠DCA=∠ECB=90°,DC=EC
∴△ACD≌△BCE(SAS)
∴∠DAC=∠EBC
∵∠ADC=∠BDF
∴∠EBC+∠BDF=∠DAC+∠ADC=90°
∴∠BFD=90°
∴AF⊥BE.
(2)解:AF⊥BE.理由如下:
∵∠ABC=∠DEC=30°,∠ACB=∠DCE=90°
∴
=
=tan60°
∴
=
,
∴△DCA∽△ECB
∴∠DAC=∠EBC
∵∠ADC=∠BDF
∴∠EBC+∠BDF=∠DAC+∠ADC=90°
∴∠BFD=90°
∴AF⊥BE.
∴△ACD≌△BCE(SAS)
∴∠DAC=∠EBC
∵∠ADC=∠BDF
∴∠EBC+∠BDF=∠DAC+∠ADC=90°
∴∠BFD=90°
∴AF⊥BE.
(2)解:AF⊥BE.理由如下:
∵∠ABC=∠DEC=30°,∠ACB=∠DCE=90°
∴
| BC |
| AC |
| EC |
| DC |
∴
| BC |
| EC |
| AC |
| DC |
∴△DCA∽△ECB
∴∠DAC=∠EBC
∵∠ADC=∠BDF
∴∠EBC+∠BDF=∠DAC+∠ADC=90°
∴∠BFD=90°
∴AF⊥BE.
点评:运用全等三角形,相似三角形同样都可以得出角相等的条件,互余关系是证明垂线的重要途径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
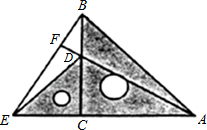 把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.试判断AF和BE的位置关系,并说明理由.
把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.试判断AF和BE的位置关系,并说明理由.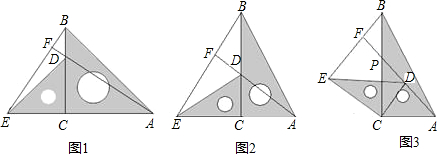
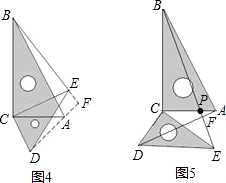
 26、把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
26、把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由. 把两个含有45°角的直角三角板如图放置,D在BC点上,连接BD、AD,AD的延长线交BE于点F,求证:AF⊥BE.
把两个含有45°角的直角三角板如图放置,D在BC点上,连接BD、AD,AD的延长线交BE于点F,求证:AF⊥BE.