题目内容
(1)异分母分式相加减,先______变为______分式,然后再加减.
(2)分式 ,
, ,
, 的最简公分母是______.
的最简公分母是______.
(3)计算: =______.
=______.
(4)计算: =______.
=______.
解:(1)异分母分式相加减,先通分变为同分母分式,然后再加减;
(2)分式 ,
, ,
, 的最简公分母是xy(x+y)(x-y);
的最简公分母是xy(x+y)(x-y);
(3)原式=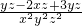 ;
;
(4)原式= •
•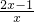 =
=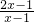 .
.
故答案为:(1)通分;同分母;(2)xy(x+y)(x-y);(3)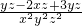 ;(4)
;(4)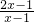
分析:(1)异分母分式相加减,先通分变为同分母分式,然后再加减;
(2)找出三个分母的最简公分母即可;
(3)通分并利用同分母分式的加减法则计算即可得到结果;
(4)原式括号中两项通分并利用同分母分式的加法法则计算,约分即可得到结果.
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.
(2)分式
 ,
, ,
, 的最简公分母是xy(x+y)(x-y);
的最简公分母是xy(x+y)(x-y);(3)原式=
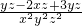 ;
;(4)原式=
 •
•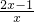 =
=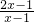 .
.故答案为:(1)通分;同分母;(2)xy(x+y)(x-y);(3)
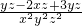 ;(4)
;(4)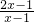
分析:(1)异分母分式相加减,先通分变为同分母分式,然后再加减;
(2)找出三个分母的最简公分母即可;
(3)通分并利用同分母分式的加减法则计算即可得到结果;
(4)原式括号中两项通分并利用同分母分式的加法法则计算,约分即可得到结果.
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目