题目内容
16．函数=$\frac{x-2}{x-5}$+$\sqrt{x-1}$的自变量x的取值范围为x≥1且x≠5．分析 根据分式有意义的条件和二次根式有意义的条件列出不等式组，求解即可．
解答 解：∵x-1≥0且x-5≠0，
∴x≥1且x≠5，
故答案为x≥1且x≠5．
点评 本题考查了函数自变量的取值范围问题，掌握分式有意义的条件和二次根式有意义的条件是解题的关键．
练习册系列答案
相关题目
6．分式方程$\frac{1}{x-2}$=$\frac{2}{x}$解为（ ）
| A． | x=-4 | B． | x=2 | C． | x=-2 | D． | x=4 |
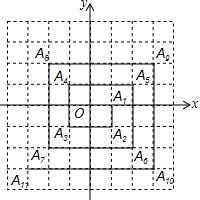如图，已知A1（1，0），A2（1，-1），A3（-1，-1），A4（-1，1），A5（2，1），…，则点A2017的坐标是（505，504）．
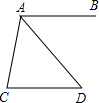如图，AB∥CD，AD平分∠BAC，且∠C=80°，则∠D的度数为50°．
1．如果反比例函数y=$\frac{k}{x}$的图象经过点（3，-2），则k的值是（ ）
| A． | -6 | B． | 6 | C． | -3 | D． | 3 |
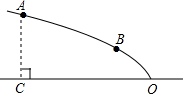如图，某广场设计的一建筑物造型的纵截面是抛物线的一部分，抛物线的顶点O落在水平面上，对称轴是水平线OC．点A、B在抛物线造型上，且点A到水平面的距离AC=4米，点B到水平面距离为2米，OC=8米．
如图所示，AO⊥BO，CO⊥DO，∠AOC：∠BOC=1：4，则∠BOD=150°．