题目内容
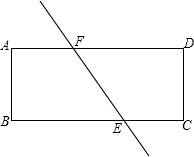
如图，直线a、b与直线c相交，给出下列条件：①∠2=∠3；②∠1=∠4；③∠1+∠4=180°．则其中能判断a∥b的是
- A.①②③
- B.①②
- C.①③
- D.只有①
C
分析：直接根据平行线的判定定理对各选项进行逐一分析．
解答：
解：①∵∠2=∠3，∴a∥b，故本小题正确；
②∵∠1=∠4，∴∠5+∠4=180°，∴无法判定a∥b，故本小题错误；
③∵∠1+∠4=180°，∠1+∠5=180°，∴∠4=∠5，∴a∥b，故本小题正确．
故选C．
点评：本题考查的是平行线的判定定理，用到的知识点为：同位角相等，两直线平行．
分析：直接根据平行线的判定定理对各选项进行逐一分析．
解答：
解：①∵∠2=∠3，∴a∥b，故本小题正确；②∵∠1=∠4，∴∠5+∠4=180°，∴无法判定a∥b，故本小题错误；
③∵∠1+∠4=180°，∠1+∠5=180°，∴∠4=∠5，∴a∥b，故本小题正确．
故选C．
点评：本题考查的是平行线的判定定理，用到的知识点为：同位角相等，两直线平行．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
如图，小明把小球竖直向上抛起，当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置，且灯与球心所在直线垂直于地面，这时小球在地面的影子的面积为1.92πm2．已知，灯与地面的距离为2.4m，小球的半径为
