题目内容
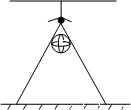
如图，小明把小球竖直向上抛起，当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置，且灯与球心所在直线垂直于地面，这时小球在地面的影子的面积为1.92πm2．已知，灯与地面的距离为2.4m，小球的半径为10
10
cm．分析：设一个切点为D，球心为O，在图中标注字母，根据圆的面积公式求出地面影子圆的半径，再利用勾股定理求出AB的长，然后利用相似三角形对应边成比例列出比例式求解即可．
解答：
解：如图，∵灯与球心所在直线垂直于地面，
∴AC⊥BC，
∵小球在地面的影子的面积为1.92πm2，
∴π•BC2=1.92π，
解得BC=
，
根据勾股定理，AB=
=
=
，
∵光线AB与球相切，
∴OD⊥AB，
∴∠ADO=∠ACB=90°，
又∵∠BAC=∠OAD，
∴△ABC∽△AOD，
∴
=
，
即
=
，
解得OD=10cm．
故答案为：10．
解：如图，∵灯与球心所在直线垂直于地面，∴AC⊥BC，
∵小球在地面的影子的面积为1.92πm2，
∴π•BC2=1.92π，
解得BC=
| 4 |
| 5 |
| 3 |
根据勾股定理，AB=
| AC2+BC2 |
| 2.42+1.92 |
| 8 |
| 5 |
| 3 |
∵光线AB与球相切，
∴OD⊥AB，
∴∠ADO=∠ACB=90°，
又∵∠BAC=∠OAD，
∴△ABC∽△AOD，
∴
| BC |
| OD |
| AB |
| AO |
即
| ||||
| OD |
| ||||
| OD+10 |
解得OD=10cm．
故答案为：10．
点评：本题考查了相似三角形的应用，切线的性质，勾股定理的应用，主要利用了相似三角形对应边成比例的性质，难点在于确定小球的半径OD不是与地面平行，而是与AB垂直．
练习册系列答案
相关题目
如图，小明把小球竖直向上抛起，当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置，且灯与球心所在直线垂直于地面，这时小球在地面的影子的面积为1.92πm2．已知，灯与地面的距离为2.4m，小球的半径为________cm．