题目内容
一个圆锥的主视图是腰长为
，顶角为150°的等腰三角形，则该圆锥的侧面积为 ．
【答案】分析：作BD⊥AC于点D，根据直角三角形中30度的锐角所对的直角边等于斜边的一半，即可求得BD的长，AD的长，在直角△BCD中，利用勾股定理即可求得BC的长，即圆锥的底面直径，然后利用扇形的面积公式即可求解．
解答：
解：作BD⊥AC于点D．
∵∠BAC=150°，
∴∠DAB=30°，
∴BD=
AB=
（
-
）=
-
，AD=
BD=
（
-
）=
-
，
∴CD=AD+AC=
-
+
-
=
+
，
在直角△ACD中，BC=
=
=2．
则圆锥的底面周长是：2π，
则圆锥的侧面积为：
×2π×（
-
）=（
-
）π．
故答案是：（
-
）π．
点评：本题考查了圆锥的计算，正确求得底面直径的长度是关键．解决此类图的关键是由三视图得到立体图形；学生由于空间想象能力不够，找不到圆锥的底面半径，或者对圆锥的侧面面积公式运用不熟练，易造成错误．
解答：
解：作BD⊥AC于点D．∵∠BAC=150°，
∴∠DAB=30°，
∴BD=
AB=（-）=-，AD=BD=（-）=-，∴CD=AD+AC=
-+-=+，在直角△ACD中，BC=
==2．则圆锥的底面周长是：2π，
则圆锥的侧面积为：
×2π×（-）=（-）π．故答案是：（
-）π．点评：本题考查了圆锥的计算，正确求得底面直径的长度是关键．解决此类图的关键是由三视图得到立体图形；学生由于空间想象能力不够，找不到圆锥的底面半径，或者对圆锥的侧面面积公式运用不熟练，易造成错误．
练习册系列答案
相关题目
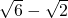，顶角为150°的等腰三角形，则该圆锥的侧面积为________．