题目内容
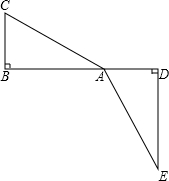
等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现△ABC以每秒2个单位的速度向右移动,同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大.
1.当△ABC的边(BC边除外)与圆第一次相切时,点B移动了多少距离?
2. 若在△ABC移动的同时,⊙O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
3.在⑵的条件下,是否存在某一时刻,△ABC与⊙O的公共部分等于⊙O的面积?若存在,求出恰好符合条件时两个图形移动了多少时间?若不存在,请说明理由.

1.假设第一次相切时,△ABC移至△A’B’C’处,A’C’与⊙O切于点E,连OE并延长,交B’C’于F.设⊙O与直线l切于点D,连OD,则OE⊥A’C’,OD⊥直线l.由切线长定理可知C’E= C’D,设C’D=x,则C’E= x,易知C’F=![]() x ∴
x ∴![]() x+x=1 ∴x=
x+x=1 ∴x=![]() -1 ∴CC’=5-1-(
-1 ∴CC’=5-1-(![]() -1)=5-
-1)=5-![]()
∴点C运动的时间为![]()
∴点B运动的的距离为![]()
2.∵△ABC与⊙O从开始运动到最后一次相切时,路程差为6,速度差为1
∴从开始运动到最后一次相切的时间为6秒
3.∵△ABC与⊙O从开始运动到第二次相切时,路程差为4,速度差为1
∴从开始运动到第二次相切的时间为4秒, 此时△ABC移至△A”B”C”处,
A”B”=1+4×![]() =3
=3
连接B”O并延长交A”C”于点P,易证B”P⊥A”C”,且OP= <1
<1
∴此时⊙O与A”C”相交
∴不存在.


解析:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
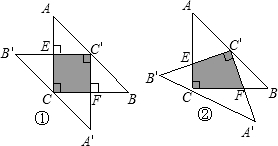 A′B′上?试说明理由.
A′B′上?试说明理由.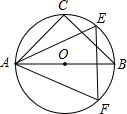 如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.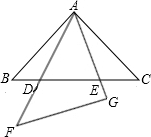 点E不与点C重合),设BE=m,CD=n.
点E不与点C重合),设BE=m,CD=n.